
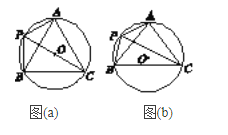
【题目】如图所示,在平面直角坐标系中,△ABC是⊙O的内接三角形,AB=AC,点P是![]() 的中点,连结PA,PB,PC.
的中点,连结PA,PB,PC.
(1)如图(a),若∠BPC=60°,求证:AC=![]() AP;
AP;
(2)如图(b),若sin∠BPC=![]() ,求tan∠PAB的值.
,求tan∠PAB的值.
【答案】(1)详见解析;(2)tan∠PAB=![]() .
.
【解析】
(1)利用已知条件易证△ABC为等边三角形,所以∠ACB=60°,因为点P是弧AB的中点,所以∠ACP=30°,进而证明AC=![]() AP;
AP;
(2)①由等腰三角形的性质可得∠BAC=2∠CAF,由圆周角定理可得∠FOC=2∠CAF,进而可证明∠FOC=∠BAC;
②过点E作EG⊥AC于G,连接OC,设FC=24a,则OC=OA=25a,因为OF=7a,AF=32a.在Rt△AFC中,AC2=AF2+FC2,所以AC=40a,进而可求出tan∠PAB的值.
解:(1)证明:∵∠BAC=∠BPC=60°.
又∵AB=AC,
∴△ABC为等边三角形,
∴∠ACB=60°,
∵点P是![]() 的中点,
的中点,
∴∠ACP=30°,
又∵∠APC=∠ABC=60°,
∴AC=![]() AP.
AP.
(2)如图,连结AO并延长交PC于点E,交BC于点F,过点E作EG⊥AC于点G,连结OC.

∵AB=AC,
∴AF⊥BC,BF=CF.
又∵点P是![]() 的中点,
的中点,
∴∠ACP=∠PCB,
∴EG=EF.
∵∠BPC=∠BAC,
又∵∠BAC=∠FOC,
∴∠BPC=∠FOC,
∴sin∠FOC=sin∠BPC=![]() .
.
设FC=24a,则OC=OA=25a,
∴OF=7a,AF=32a.
在Rt△AFC中,AC2=AF2+FC2,∴AC=40a.
在Rt△AGE和Rt△AFC中,sin∠FAC=![]() ,
,
∴![]() ,∴EG=12a.
,∴EG=12a.
∴tan∠PAB=tan∠PCB=![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】(已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是( )
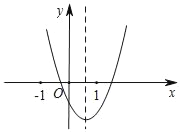
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
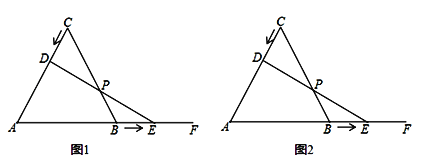
【题目】知识链接:将两个含30°角的全等三角尺放在一起,让两个30°角合在一起成60°,经过拼凑、观察、思考,探究出“直角三角形中30°角所对的直角边等于斜边的一半”结论.
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P,设运动时间为x秒.
(1)请直接写出AD长.(用x的代数式表示)
(2)当△ADE为直角三角形时,运动时间为几秒?
(2)求证:在运动过程中,点P始终为线段DE的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
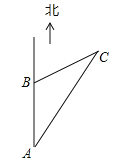
【题目】一艘轮船沿正北方向航行,在A处测得北偏东21.3°方向有一座小岛C,继续向北航行60海里到达B处,测得小岛C此时在轮船的北偏东63.5°方向上.之后,轮船继续向北航行多少海里,距离小岛C最近?
(参考数据:sin21.3°≈![]() ,tan21.3°≈
,tan21.3°≈![]() ,sin63.5°≈
,sin63.5°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 分别在矩形
分别在矩形![]() 边
边![]() 、
、![]() 、
、![]() 上,
上,![]() .
.
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为正方形时,求
为正方形时,求![]() 的面积;
的面积;
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为菱形时,设
为菱形时,设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在AB上,![]() 、
、![]() 均是等边三角形,
均是等边三角形,![]() 、
、![]() 分别与
分别与![]() 交于点
交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() 为等边三角形;④
为等边三角形;④![]() ∥
∥![]() ;⑤DC=DN正确的有( )个
;⑤DC=DN正确的有( )个
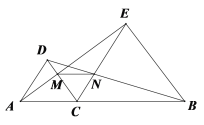
A.2个B.3个C.4个D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
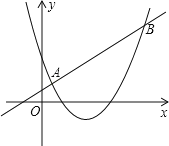
【题目】已知一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图所示,它们的两个交点的横坐标是1和4,那么能够使得y1<y2的自变量x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com