
【题目】 如图,E为正方形ABCD边AB上一动点(不与A重合),AB=4,将△DAE绕着点A逆时针旋转90°得到△BAF,再将△DAE沿直线DE折叠得到△DME.下列结论:①连结AM,则AM∥FB;②连结FE,当F、E、M共线时,AE=4![]() -4;③连结EF、EC、FC,若△FEC是等腰三角形,则AE=4
-4;③连结EF、EC、FC,若△FEC是等腰三角形,则AE=4![]() -4;④连结EF,设FC、ED交于点O,若FE平分∠BFC,则O是FC的中点,且AE=2
-4;④连结EF,设FC、ED交于点O,若FE平分∠BFC,则O是FC的中点,且AE=2![]() -2,其中正确的个数有( )个.
-2,其中正确的个数有( )个.

A.4B.3C.2D.1
【答案】A
【解析】
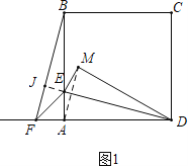
①正确.如图1中,连接AM,延长DE交BF于J.想办法证明BF⊥DJ,AM⊥DJ即可.
②正确.如图2中,当F、E、M共线时,易证∠DEA=∠DEM=67.5°,在MD上取一点J,使得ME=MJ,连接EJ,设AE=EM=MJ=x,则EJ=JD=![]() x,构建方程即可解决问题.
x,构建方程即可解决问题.
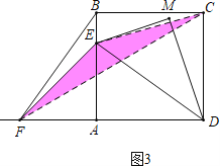
③正确.如图3中,连接EC,CF,当EF=CE时,设AE=AF=m,利用勾股定理构建方程即可解决问题.
④正确.如图4中,当OF=OC时,设AE=AF=n.根据tan∠CFD=tan∠EDA,构建方程即可解决问题.
解:①如图1中,连接AM,延长DE交BF于J.
∵四边形ABCD是正方形,
∴AB=AD.∠DAE=∠BAF=90°,
∵AE=AF,
∴△BAF≌△DAE(SAS),
∴∠ABF=∠ADE,
∵∠ADE+∠AED=90°,∠AED=∠BEJ,
∴∠BEJ+∠EBJ=90°,
∴∠BJE=90°,
∴DJ⊥BF,
由翻折可知:EA=EM,DM=DA,
∴DE垂直平分线段AM,
∴BF∥AM,故①正确,
②如图2中,当F、E、M共线时,易证∠DEA=∠DEM=67.5°,
在MD上取一点J,使得ME=MJ,连接EJ,

∵∠MEJ=∠MJE=45°,
∴∠JED=∠JDE=22.5°,
∴EJ=JD,设AE=EM=MJ=x,则EJ=JD=![]() x,
x,
则有x+![]() x=4,
x=4,
∴x=4![]() -4,
-4,
∴AE=4![]() -4故②正确,
-4故②正确,
③如图3中,连接EC,CF,当EF=CE时,设AE=AF=m,
则有:2m2=42+(4-m)2,
∴m=4![]() -4或-4
-4或-4![]() -4(舍弃),
-4(舍弃),
∴AE=4![]() -4,故③正确,
-4,故③正确,
④如图4中,当OF=OC时,设AE=AF=n.

∵∠FDC=90°,OF=OC,
∴OF=OD,
∴∠OFD=∠ODF,
∴tan∠CFD=tan∠EDA,
,![]() =
=![]() ,
,
∴n=2![]() -2或-2
-2或-2![]() -2(舍弃),
-2(舍弃),
∴AE=2![]() -2,故④正确.
-2,故④正确.
故选:A.


科目:初中数学 来源: 题型:
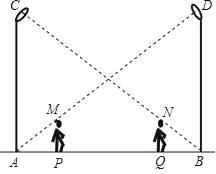
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+4x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
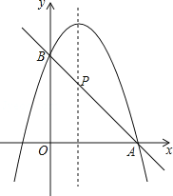
(2)如图,二次函数的图象过点A(6,0),与y轴交于点B,点p是二次函数对称轴上的一个动点,当PB+PA的值最小时,求p的坐标
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场篮球比赛中,一名球员在关键时刻投出一球,已知球出手时离地面高2米,与篮圈中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,已知篮球运行的轨迹为抛物线,篮圈中心距离地面3.19米.
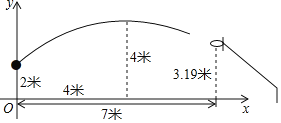
(1)以地面为x轴,篮球出手时垂直地面所在直线为y轴建立平面直角坐标系,求篮球运行的抛物线轨迹的解析式;
(2)通过计算,判断这个球员能否投中?
查看答案和解析>>
科目:初中数学 来源: 题型:
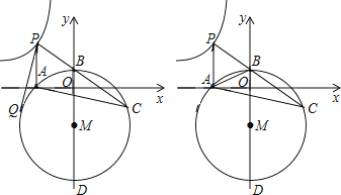
【题目】 如图,点P在曲线y=![]() (x<0)上,PA⊥x轴于点A,点B在y轴正半轴上,PA=PB,OA、OB的长是方程t2-8t+12=0的两个实数根,且OA>OB,点C是线段PB延长线上的一个动点,△ABC的外接圆⊙M与y轴的另一个交点是D.
(x<0)上,PA⊥x轴于点A,点B在y轴正半轴上,PA=PB,OA、OB的长是方程t2-8t+12=0的两个实数根,且OA>OB,点C是线段PB延长线上的一个动点,△ABC的外接圆⊙M与y轴的另一个交点是D.
(1)填空:OA=______;OB=______;k=______.
(2)设点Q是⊙M上一动点,若圆心M在y轴上且点P、Q之间的距离达到最大值,则点Q的坐标是______;
(3)试问:在点C运动的过程中,BD-BC的值是否为定值?若是,请求出该定值;若不是,请给出合理的解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
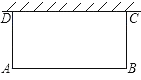
【题目】如图,利用一面墙(墙的长度不超过45米),用80米长的篱笆围一个矩形场地.
(1)设所围矩形ABCD的边AB为x米,则边BC= 米;
(2)怎样围才能使矩形场地的面积为750米2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com