
【题目】如图,在平面直角坐标系中,已知点A(﹣1, ![]() ),B(2,0)在抛物线11:y=ax2+bx+1(a,b为常数,且a≠0)上,直线12经过抛物线11的顶点且与y轴垂直,垂足为点D.
),B(2,0)在抛物线11:y=ax2+bx+1(a,b为常数,且a≠0)上,直线12经过抛物线11的顶点且与y轴垂直,垂足为点D.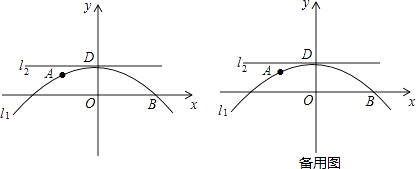
(1)求l1的解析式,并写出它的对称轴和顶点坐标;
(2)设l1上有一动点P从点A出发,沿抛物线从左向右运动,点P的纵坐标yp也随之以每秒2个单位长的速度变化,设点P运动的时间为t(秒),连接OP,以线段OP为直径作⊙F.
①求yp关于t的表达式,并写出t的取值范围;
②当点P在起点A处时,直线l2与⊙F的位置关系是 , 在点P从点A运动到点D的过程中,直线12与⊙F是否始终保持着上述的位置关系?请说明理由;
(3)在(2)条件下,当点P开始从点A出发,沿抛物线从左到右运动时,直线l2同时向下平移,垂足D的纵坐标yD以每秒3个单位长度速度变化,当直线l2与⊙F相交时,求t的取值范围.
【答案】
(1)
解:把点A(﹣1, ![]() ),B(2,0)代入抛物线11:y=ax2+bx+1中得:
),B(2,0)代入抛物线11:y=ax2+bx+1中得:
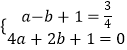 解得
解得 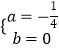 ,
,
∴y=﹣ ![]() x2+1 则对称轴为:直线x=0,顶点为(0,1)
x2+1 则对称轴为:直线x=0,顶点为(0,1)
(2)相切
(3)
解:设点P坐标(m,﹣ ![]() m2+1),则点F坐标(
m2+1),则点F坐标( ![]() m,﹣
m,﹣ ![]() m2+
m2+ ![]() ),
),
∵OP= ![]() =
= ![]() m2+1,
m2+1,
∴⊙F的半径= ![]() m2+
m2+ ![]() ,
,
∴直线y=﹣ ![]() m2+
m2+ ![]() ﹣(
﹣( ![]() m2+
m2+ ![]() )=﹣
)=﹣ ![]() m2与⊙F相切,
m2与⊙F相切,
∵t> ![]() 时,﹣
时,﹣ ![]() m2+1=1﹣2(t﹣
m2+1=1﹣2(t﹣ ![]() ),
),
∴﹣ ![]() m2=﹣2t+
m2=﹣2t+ ![]() ,
,
当1﹣3t=﹣2t+ ![]() 时直线l2与⊙F相切,解得t=
时直线l2与⊙F相切,解得t= ![]() ,
,
∴当0<t< ![]() 时,⊙F与直线l2相交
时,⊙F与直线l2相交
【解析】解:(2)①由题意1﹣ ![]() =2t解得t=
=2t解得t= ![]() ,
,
∴0≤t ![]() 时,yP=
时,yP= ![]() +2t,
+2t,
t> ![]() 时,yP=1﹣2(t﹣
时,yP=1﹣2(t﹣ ![]() )=
)= ![]() ﹣2t.
﹣2t.
②当点P在起点A处时,OA= ![]() =
= ![]() ,
,
∴⊙F的半径为 ![]() ,
,
∵点F坐标(﹣ ![]() ,
, ![]() ),
),
∴点F到直线y=1的距离为 ![]() ,
,
∴点F到直线y=1的距离等于⊙F的半径,
∴直线l2与⊙F相切,
所以答案是相切.
结论:在点P从点A运动到点D的过程中,直线12与⊙F始终保持相切.
理由:设点P坐标(m,﹣ ![]() m2+1),则点F坐标(
m2+1),则点F坐标( ![]() m,﹣
m,﹣ ![]() m2+
m2+ ![]() ),
),
∵OP= ![]() =
= ![]() m2+1,
m2+1,
∴⊙F的半径= ![]() m2+
m2+ ![]() ,
,
∵点F到直线y=1的距离为1﹣(﹣ ![]() m2+
m2+ ![]() )=
)= ![]() m2+
m2+ ![]() ,
,
∴点F到直线y=1的距离等于⊙F的半径,
∴在点P从点A运动到点D的过程中,直线12与⊙F始终保持相切.


科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C是数轴上三点,O为原点,点C对应的数为3,BC=2,AB=6.
(1)求点A,B对应的数;
(2)动点M,N分别同时从AC出发,分别以每秒3个单位和1个单位的速度沿数轴正方向运动.P为AM的中点,Q在CN上,且CQ=![]() CN,设运动时间为t(t > 0).
CN,设运动时间为t(t > 0).
①求点P,Q对应的数(用含t的式子表示);
②t为何值时OP=BQ.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青山村种的水稻2010年平均每公顷产7200kg,2012年水稻平均每公顷产的产量是8400kg,设水稻每公顷产量的年平均增长率为x,可列方程为( )
A.7200(1+x)2=8400B.7200(1+x2)=8400
C.7200(x2+x)=8400D.7200(1+x)=8400
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】x表示一个两位数,y表示一个三位数,如果把x放在y的左边组成一个五位数,那么这个五位数就可以表示为( )
A.xy
B.x+y
C.1 000x+y
D.10x+y
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( ) 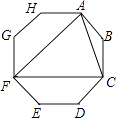
A.△ACF是等边三角形
B.连接BF,则BF分别平分∠AFC和∠ABC
C.整个图形是轴对称图形,但不是中心对称图形
D.四边形AFGH与四边形CFED的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人和人之间讲友情,有趣的是,数与数之间也有相类似的关系. 若两个不同的自然数的所有真因数(即除了自身以外的正约数)之和相等,我们称这两个数为“亲和数”. 例如:18的约数有1、2、3、6、9、18,它的真因数之和1+2+3+6+9=21;51的约数有1、3、17、51,它的真因数之和1+3+17=21,所以18和51为“亲和数”. 数还可以与动物形象地联系起来,我们称一个两头(首位与末位)都是![]() 的数为“两头蛇数”.
的数为“两头蛇数”.
(1)6的“亲和数”为 ;将一个四位的“两头蛇数”去掉两头,得到一个两位数,它恰好是这个“两头蛇数”的约数,求满足条件的“两头蛇数”.
(2)已知两个“亲和数”的真因数之和都等于15,且这两个“亲和数”中较大的数能将一个正中间数位(百位)上的数为4的五位“两头蛇数”整除,若这个五位“两头蛇数”的千位上的数字小于十位上的数字,求满足条件的“两头蛇数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com