
| A. | m-2>n+2 | B. | 2m>2n | C. | -$\frac{m}{2}$>$\frac{n}{2}$ | D. | m2>n2 |
分析 根据不等式的性质:不等式的两边都加(或减)同一个数,不等号的方向不变,不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;不等式的两边都乘以(或除以)同一个负数,不等号的方向改变,可得答案.
解答 解:A、左边减2,右边2,故A错误;
B、两边都乘以2,不等号的方向不变,故B正确;
C、左边除以-2,右边除以2,故C错误;
D、两边乘以不同的数,故D错误;
故选:B.
点评 本题考查了不等式的性质,不等式的基本性质是解不等式的主要依据,必须熟练地掌握.要认真弄清不等式的基本性质与等式的基本性质的异同,特别是在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于0,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.


科目:初中数学 来源: 题型:填空题
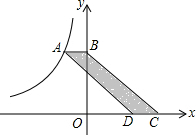 如图,在平面直角坐标系中,点A是函数y=$\frac{k}{x}$(k<0,x<0)图象上的点,过点A与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为-3.
如图,在平面直角坐标系中,点A是函数y=$\frac{k}{x}$(k<0,x<0)图象上的点,过点A与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
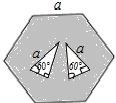 如图,边长为a的正六边形内有两个三角形(数据如图),则$\frac{{S}_{空白}}{{S}_{阴影}}$=$\frac{1}{5}$.
如图,边长为a的正六边形内有两个三角形(数据如图),则$\frac{{S}_{空白}}{{S}_{阴影}}$=$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{6}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
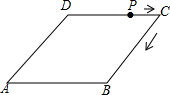 如图,菱形ABCD的边长为4,∠A=30°,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,△ADP的面积为y,则y关于x的函数图象是( )
如图,菱形ABCD的边长为4,∠A=30°,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为x,△ADP的面积为y,则y关于x的函数图象是( )| A. | 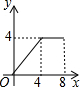 | B. | 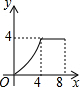 | C. | 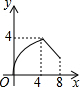 | D. | 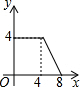 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com