
【题目】定义:对于平面直角坐标系中的任意直线MN及点P,取直线MN上一点Q,线段PQ与直线MN成30°角的长度称为点P到直线MN的30°角的距离,记作d(P→MN).
已知O为坐标原点,A(4,0),B(3,3)是平面直角坐标系中两点.根据上述定义,解答下列问题:
(1)点A到直线OB的30°角的距离d(A→OB)=;
(2)已知点G到线段OB的30°角的距离d(G→OB)=2,且点G的横坐标为1,则点G的纵坐标为 .
(3)若点A到直线l:y=kx+1的30°角的距离d(A→l)=4,求k的值.
【答案】
(1)4 ![]()
(2)1+ ![]() 或1﹣
或1﹣ ![]()
(3)
解:如图3中,作AF⊥直线l:y=kx+1于F,直线l交x轴于H,交y轴于G,设H(m,0),

易知OG=1,AE=4,AF=2,OA=4,
由△HOG∽△HFA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
解得m= ![]() 或
或 ![]() (舍弃),
(舍弃),
∴H( ![]() ,0),代入y=kx+1,得到k=
,0),代入y=kx+1,得到k= ![]() =
= ![]() =
= ![]() ,
,
当直线l经过一、二、四象限如图所示,同法可得k=﹣ ![]() =﹣
=﹣ ![]() .
.
【解析】解:(1)如图1中,作AF⊥OB于F,在OB上取一点E,使得∠AEF=30°,则d(A→OB)=AE.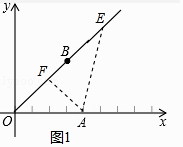
∵B(3,3),
∴∠AOF=∠OAF=45°,
∵OA=4,
∴AF=OF=2 ![]() ,
,
在Rt△AEF中,AE=2AF=4 ![]() .
.
所以答案是4 ![]() .(2)如图2中,作GF⊥OB于F,∠GEO=30°,GE=2,
.(2)如图2中,作GF⊥OB于F,∠GEO=30°,GE=2,
∴FG= ![]() EG=1,
EG=1,
设直线x=1与直线OB交于点H,与x轴交于M,
∵∠GHF=∠HGF=45°,OM=HM=1,GF=HF=1,
∴GH= ![]() ,
,
∴G(1,1+ ![]() ),
),
当G在直线OB下方时,同法可得G′(1,1﹣ ![]() ),
),
所以答案是1+ ![]() 或1﹣
或1﹣ ![]() .
.
【考点精析】关于本题考查的两点间的距离,需要了解同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在多边形ABCDE中,∠A=∠AED=∠D=90°,AB=5,AE=2,ED=3,过点E作EF∥CB交AB于点F,FB=1,过AE上的点P作PQ∥AB交线段EF于点O,交折线BCD于点Q,设AP=x,POOQ=y.
(1)①延长BC交ED于点M,则MD= , DC=;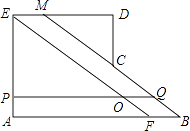
(2)求y关于x的函数解析式;
(3)当a≤x≤ ![]() (a>0)时,9a≤y≤6b,求a,b的值;
(a>0)时,9a≤y≤6b,求a,b的值;
(4)当1≤y≤3时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上 的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据: ![]() ≈1.73).
≈1.73).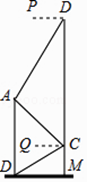
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在反比例函数y= ![]() (x>0)图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA到点D,使AD=
(x>0)图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA到点D,使AD= ![]() AB,延长BA到点E,使AE=
AB,延长BA到点E,使AE= ![]() AC,直线DE分别交x、y轴于点P、Q,当
AC,直线DE分别交x、y轴于点P、Q,当 ![]() =
= ![]() 时,则△ACE与△ADB面积之和等于 .
时,则△ACE与△ADB面积之和等于 . 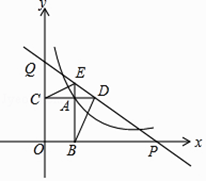
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,2)、B(﹣5,0)、C(﹣1,0),P(a,b)是△ABC的边AC上一点:
(1)将△ABC绕原点O逆时针旋转90°得到△A1B1C1 , 请在网格中画出△A1B1C1 , 旋转过程中点A所走的路径长为 ![]() .
.
(2)将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2 , 并写出点A2的坐标:A2().
(3)若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() (x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com