
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
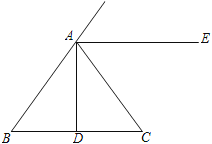
(1)作∠ADC的平分线DF,与AE交于点F;(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AD=2,求DF的长.
科目:初中数学 来源: 题型:
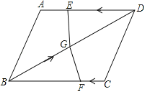
【题目】如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
(1)试证明:AD∥BC.
(2)在移动过程中,小芹发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校图书馆大楼工程在招标时,接到甲乙两个工程队的投标书,每施工一个月,需付甲工程队工程款16万元,付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成此项工程刚好如期完工;
(2)乙队单独完成此项工程要比规定工期多用3个月;
(3)若甲乙两队合作2个月,剩下的工程由乙队独做也正好如期完工。
你觉得哪一种施工方案最节省工程款,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(﹣1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向 A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二: 同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受 9 折优惠的概率为_______;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知关于x的方程2x2﹣mx﹣m2=0有一个根是1,求m的值;
(2)已知关于x的方程(2x﹣m)(mx+1)=(3x+1)(mx﹣1)有一个根是0,求另一个根和m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:


如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com