
【题目】如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(﹣1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为 .

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
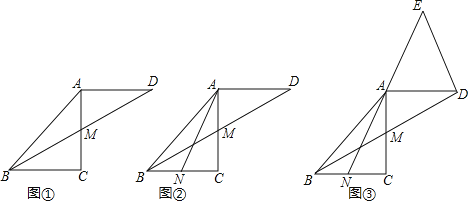
【题目】已知△ABC是等腰直角三角形,∠C=90°,点M是AC的中点,延长BM至点D,使DM=BM,连接AD.
(1)如图①,求证:△DAM≌△BCM;
(2)已知点N是BC的中点,连接AN.
①如图②,求证:△BCM≌△ACN;
②如图③,延长NA至点E,使AE=NA,连接DE.求证:BD⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
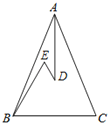
【题目】如图所示,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC≡∠E=60°,若BE=10,DE=4,则BC的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,

(1)求证:△ABQ ≌ △CAP;
(2)∠CMQ的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)连接PQ,当点P,Q运动多少秒时,△PBQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M,N分别在BC,AC上,且BM=CN现有以下四个结论:
①DN=DM; ② ∠NDM=90°; ③ 四边形CMDN的面积为4; ④△CMN的面积最大为2.
其中正确的结论有( )

A. ①②④; B. ①②③; C. ②③④; D. ①②③④.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
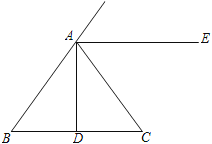
(1)作∠ADC的平分线DF,与AE交于点F;(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AD=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品![]() 件(
件(![]() >0),购买两种商品共花费
>0),购买两种商品共花费![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式(写出自变量
的函数关系式(写出自变量![]() 的取值范围);
的取值范围);
(2)试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】妈妈在超市购买两种优质水果.先购买了2千克甲水果和3千克乙水果,共花费90元;后又购买了1千克甲水果和2千克乙水果,共花费55元.(每次两种水果的售价都不变)
(1)求甲水果和乙水果的售价分别是每千克多少元;
(2)如果还需购买两种水果共12千克,要求乙水果的数量不少于甲水果数量的2倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com