
【题目】已知△ABC是等腰直角三角形,∠C=90°,点M是AC的中点,延长BM至点D,使DM=BM,连接AD.
(1)如图①,求证:△DAM≌△BCM;
(2)已知点N是BC的中点,连接AN.
①如图②,求证:△BCM≌△ACN;
②如图③,延长NA至点E,使AE=NA,连接DE.求证:BD⊥DE.
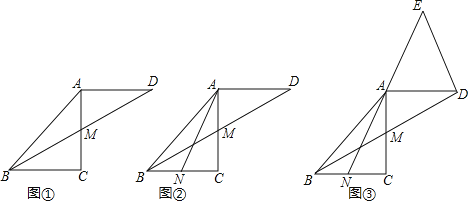
【答案】(1)见解析;(2)①见解析;②见解析.
【解析】
(1)利用SAS进行证明即可;
(2)由点M是AC的中点,点N是BC的中点,AC=BC,可得CM=CN,继而利用SAS进行证明即可;
②取AD中点F,连接EF,则AD=2AF,由△BCM≌△ACN,△DAM≌△BCM,可推导得出AF=CN,∠EAF=∠ANC,根据SAS可证明△EAF≌△ANC,从而可得∠NAC=∠AEF,∠C=∠AFE=90°,进而可得∠AFE=∠DFE=90°,继而可以证明△AFE≌△DFE,则有∠EAD=∠EDA=∠ANC,继而可得∠EDB=90°,问题得证.
(1)∵点M是AC的中点,∴AM=CM,
在△DAM和△BCM中,
∵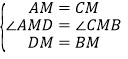 ,∴△DAM≌△BCM(SAS);
,∴△DAM≌△BCM(SAS);
(2)①∵点M是AC的中点,点N是BC的中点,∴CM=![]() AC,CN=
AC,CN=![]() BC,
BC,
∵△ABC是等腰直角三角形,∴AC=BC,∴CM=CN,
在△BCM和△ACN中,∵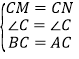 ,∴△BCM≌△ACN(SAS);
,∴△BCM≌△ACN(SAS);
②取AD中点F,连接EF,

则AD=2AF,
∵△BCM≌△ACN,∴AN=BM,∠CBM=∠CAN,
∵△DAM≌△BCM,∴∠CBM=∠ADM,AD=BC=2CN,
∴AF=CN,∴∠DAC=∠C=90°,∠ADM=∠CBM=∠NAC,
∴AD∥BC,∴∠EAF=∠ANC.
在△EAF和△ANC中,∵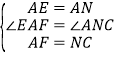 ,∴△EAF≌△ANC(SAS),
,∴△EAF≌△ANC(SAS),
∴∠NAC=∠AEF,∠C=∠AFE=90°,∴∠AFE=∠DFE=90°,
∵F为AD的中点,∴AF=DF,
在△AFE和△DFE中,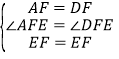 ,
,
∴△AFE≌△DFE(SAS),
∴∠EAD=∠EDA=∠ANC,
∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°–∠DAM=180°–90°=90°,
∴BD⊥DE.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
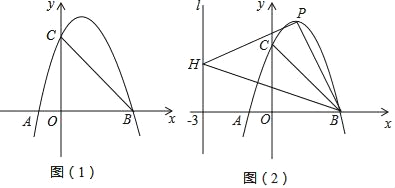
【题目】如图(1),已知抛物线E:y=ax2+bx+c与x轴交于A,B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),对称轴为直线x=1.
(1)填空:a= ,b= ,c= ;
(2)将抛物线E向下平移d个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求d的取值范围;
(3)如图(2),设点P是抛物线E上任意一点,点H在直线x=﹣3上,△PBH能否成为以点P为直角顶点的等腰直角三角形?若能,请求出符合条件的点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=6,AB=10,点D是边BC上一点.若沿AD将△ACD翻折,点C刚好落在AB边上点E处,则AD= _______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家今年种植的“夏黑”葡萄喜获丰收,采摘上市后若干天便全部销完.小明对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(千克)与上市时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少15千克.
(1)第16天的日销售量是 千克.
(2)求y与x之间的函数关系式,并写出x的取值范围;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字6,﹣2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于10的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
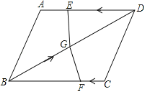
【题目】如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.
(1)试证明:AD∥BC.
(2)在移动过程中,小芹发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
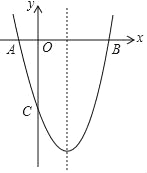
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(﹣1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com