

���� ��1����ͼ1�У����ۣ�AD+BE=AB����CH��AB��H��ֻҪ֤����ACD�ա�ACH����BCH�ա�BCE���ɣ�
��2����ͼ2�У���1�������ý����Ƿ���Ȼ���������߶�AB�Ͻ�ȡAF=AD������FC��ֻҪ֤����ADC�ա�AFC��SAS������CBF�ա�CBE��AAS�����ɽ�����⣮
��3������������ͼ3�У����ۣ�AD-BE=AB���ӳ�BC��AM��F��ֻҪ֤����ABF�ǵ��������Σ���CDF�ա�CEB�����ɽ�����⣮��ͼ4�У����ۣ�BE-AD=AB��֤���������ƣ�
��� �⣺��1�����ۣ�AD+BE=AB����ȫͼ�Σ���ͼ1��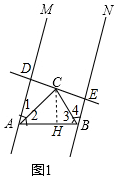
���ɣ���CD��AM��CH��AB��
���ADC=��CHA=90�㣬
�ڡ�ACD�͡�ACH�У�
$\left\{\begin{array}{l}{��1=��2}\\{��ADC=��AHC}\\{AC=AC}\end{array}\right.$��
���ACD�ա�ACH��AAS����
��AD=AH��
ͬ����֤��BCH�ա�BCE��
��BH=BE��
��AD+BE=AH+BH=AB��
��2����1�������ý����Ƿ���Ȼ������
֤������ͼ2�У����߶�AB�Ͻ�ȡAF=AD������FC��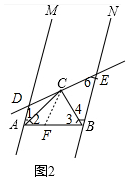
��AC��BC�ֱ�ƽ�֡�MAB����NBA��
���1=��2����3=��4��
�ڡ�ADC�͡�AFC�У�
$\left\{\begin{array}{l}AD=AF\\��1=��2\\ AC=AC�������ߣ�\end{array}\right.$��
���ADC�ա�AFC��SAS����
���ADC=��AFC��
��MA��NB��
���ADC+��6=180�㣬
�֡ߡ�5+��AFC=180�㣬
���5=��6��
�ڡ�CBF�͡�CBE�У�
$\left\{\begin{array}{l}��5=��6\\��3=��4\\ BC=BC�������ߣ�\end{array}\right.$��
���CBF�ա�CBE��AAS����
��BF=BE
��AF+BF=AB��
��AD+BE=AB��
��3����������
��ͼ3�У����ۣ�AD-BE=AB��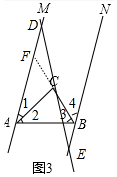
���ɣ��ӳ�BC��AM��F��
��AD��BN��
���4=��AFB=��3����FDC=��CEB��
��AF=AB��
�ߡ�1=��2��
��AC��BF��CF=BC��
�ڡ�CDF�͡�CEB�У�
$\left\{\begin{array}{l}{��CDF=��CEB}\\{��FCD=��ECB}\\{CF=BC}\end{array}\right.$��
���CDF�ա�CEB��
��DF=BE��
��AD-BE=AD=AF=AF=AB��
��AD=BE=AB��
��ͼ4�У����ۣ�BE-AD=AB����֤����������ͼ3���Σ���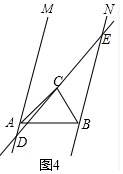
���� ���⿼���������ۺ��⡢��ƽ���ߵ����ʶ��������������ε��ж������ʡ�ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬�����п��������ͣ�


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��C��D����ABΪֱ����ԲO�ϵ��������㣨��C��D����A��B�غϣ������˶���������CDʼ�ձ��ֲ��䣬M����CD���е㣬����C��CP��AB�ڵ�P����CD=3��AB=5��PM=x����x�����ֵ�ǣ�������
��ͼ��C��D����ABΪֱ����ԲO�ϵ��������㣨��C��D����A��B�غϣ������˶���������CDʼ�ձ��ֲ��䣬M����CD���е㣬����C��CP��AB�ڵ�P����CD=3��AB=5��PM=x����x�����ֵ�ǣ�������| A�� | 3 | B�� | $\sqrt{5}$ | C�� | 2.5 | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1152�� | B�� | 576�� | C�� | 288�� | D�� | 144�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��ֱ��m��һ�κ���y=kx+b��ͼ��
��ͼ��ʾ��ֱ��m��һ�κ���y=kx+b��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����B��ֱ��l������һ�㣬AB��BC��B����AB=BC������仭ͼ���ش����⣮
��ͼ����B��ֱ��l������һ�㣬AB��BC��B����AB=BC������仭ͼ���ش����⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��O��������ABCD�����ģ�M��ABCD��һ�㣬��DMC=90�㣬����DMC��O����ת180���õ���NAB����MD=3��CM=4����MN�ij�Ϊ$\sqrt{2}$��
��ͼ��O��������ABCD�����ģ�M��ABCD��һ�㣬��DMC=90�㣬����DMC��O����ת180���õ���NAB����MD=3��CM=4����MN�ij�Ϊ$\sqrt{2}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com