
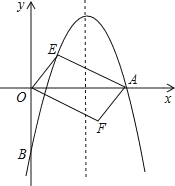
【题目】如图,对称轴为直线x=的抛物线经过点A(6,0)和B(0,﹣4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
【答案】(1)y=-x2+x-4,顶点坐标(,);(2)S=-2x2+14x-12;(3)不能.
【解析】
试题分析:(1)根据对称轴,以及A、B坐标可求得解析式,进而可求顶点坐标;(2)根据平行四边形的面积公式,可得函数解析式;(3)根据函数值,可得E点坐标,根据菱形的判定,可得答案.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c,将A、B点的坐标代入函数解析式,得 ,解得
,解得 ,抛物线的解析式为y=- x2+x-4=﹣(x﹣)2+,∴解析式为y=-x2+x-4,顶点坐标(,);(2)E点坐标为(x,-x2+x-4),S=2×OAyE=3(-x2+x-4),即S=﹣2x2+14x﹣12;
,抛物线的解析式为y=- x2+x-4=﹣(x﹣)2+,∴解析式为y=-x2+x-4,顶点坐标(,);(2)E点坐标为(x,-x2+x-4),S=2×OAyE=3(-x2+x-4),即S=﹣2x2+14x﹣12;
(3)平行四边形OEAF的面积为24时,平行四边形OEAF不能为菱形,理由如下:当平行四边形OEAF的面积为24时,即﹣2x2+14x﹣12=24,x2﹣7x+18=0,∴△=b2﹣4ac=(﹣7)2﹣4×18=﹣23<0,方程无解,
E点不存在,平行四边形OEAF的面积为24时,平行四边形OEAF不能为菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】探索规律,观察下面算式,解答问题.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)请猜想:1+3+5+7+9+…+19=________;
(2)请猜想:1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=________;
(3)试计算:101+103+…+197+199.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A.3ax2﹣6ax=3 (ax2﹣2ax)B.x2+y2=(﹣x+y)(﹣x﹣y)
C.a2+2ab﹣4b2=(a+2b)2D.ax2﹣2ax+a=a (x﹣1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
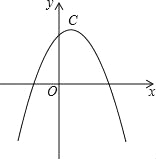
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①直线外一点到这条直线的垂线段,叫做点到直线的距离;②两点之间线段最短;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中,真命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com