
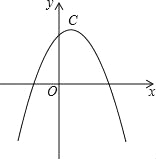
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��y1=��2x2+4x+2��C2��u2=��x2+mx+nΪ���Ѻ������ߡ���
��1����������C2�Ľ���ʽ��
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
��3����������C2�Ķ���ΪC����B������Ϊ����1��4��������C2�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������C2�ϣ������������M�����꣬������˵�����ɣ�
���𰸡���1��u2=��x2+2x+3����2��![]() ����3��M��1��2����1��5��.
����3��M��1��2����1��5��.
��������
�����������1�������C1���㣬�ٸ������������Ѻ�������������ֱ�ӵó�C2�Ķ���ʽ���ٻ���һ��ʽ���ɣ���2�����ú��������ֵ������A��a����a2+2a+3������OQ=x��AQ=��a2+2a+3���õ�OQ+AQ��a�ĺ�����ϵʽ�������ú�����ֵ���OQ+AQ����ֵ����3������BC������B����B��D��CM������ΪD������BCM�ա�MDB��������BC=MD��CM=B��D�����M������Ϊ��1��a������ʾ����B�������꣬����B����������������ߵĽ���ʽ�����a��ֵ���Ӷ��õ���M�����꣮
��������� ��1����y1=��2x2+4x+2=��2��x��1��2+4����������C1�Ķ�������Ϊ��1��4������������C1��C2������ͬ���� u2=����x��1��2+4=��x2+2x+3����������C2�Ľ���ʽΪu2=��x2+2x+3����2����ͼ1�� ���A������Ϊ��a����a2+2a+3������AQ=��a2+2a+3��OQ=a����AQ+OQ=��a2+2a+3+a=��a2+3a+3=![]() ��
��
����a=![]() ʱ��AQ+OQ�����ֵ�����ֵΪ
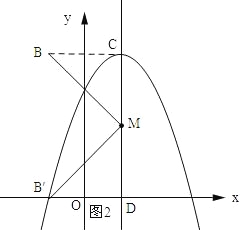
ʱ��AQ+OQ�����ֵ�����ֵΪ![]() ����3����ͼ2������BC������B����B��D��CM������ΪD��
����3����ͼ2������BC������B����B��D��CM������ΪD��
��B����1��4����C��1��4���������ߵĶԳ���Ϊx=1����BC��CM��BC=2���ߡ�BMB��=90�������BMC+��B��MD=90����
��B��D��MC�����MB��D+��B��MD=90�������MB��D=��BMC����BM=B��M�����BCM�ա�MDB������BC=MD��CM=B��D��
���M������Ϊ��1��a������B��D=CM=4��a��MD=CB=2������B��������Ϊ��a��3��a��2�����ੁ��a��3��2+2��a��3��+3=a��2�����a1=2��a2=5����a=2ʱ��M������Ϊ��1��2������a=5ʱ��M������Ϊ��1��5����
������������M������Ϊ��1��2����1��5��ʱ��B��ǡ������������C2�ϣ�




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���A��ʾ������4����B���A�ľ�����5�����B��ʾ������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ���ǣ� ��
A.3x+2y=5xy
B.4x��3x=1
C.ab��2ab=��ab
D.2a+a=2a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
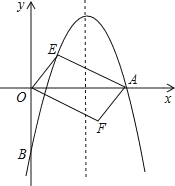
����Ŀ����ͼ���Գ���Ϊֱ��x=�������߾�����A��6��0����B��0����4����
��1���������߽���ʽ���������ꣻ
��2�����E��x��y������������һ���㣬��λ�ڵ�һ���ޣ��ı���OEAF����OAΪ�Խ��ߵ�ƽ���ı��Σ���ƽ���ı���OEAF�����S��x֮��ĺ�����ϵʽ��
��3������2���е�ƽ���ı���OEAF�����Ϊ24ʱ�����ж�ƽ���ı���OEAF�Ƿ�Ϊ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������ε��ڽǺ�Ϊ540��,����������Ϊ
A��������B���ı���C�������D��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=2x2 - 4x+c������(2, -3),��c��ֵΪ( )
A.-1B.2C.-3D.-2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABN����ACMλ����ͼ��ʾ��AB=AC��AD=AE����1=��2��
��1����֤��BD=CE��
��2����֤����M=��N��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com