
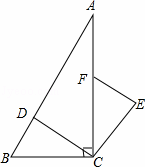
如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证: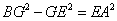 .
.

(1)BH=AC,理由如下:
 ∵CD⊥AB,BE⊥AC,
∵CD⊥AB,BE⊥AC,
∴∠BDH=∠BEC=∠CDA=90°,
∵∠ABC=45°,
∴∠BCD=180°-90°-45°=45°=∠ABC
∴DB=DC,
∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°,
∴∠HBD=∠ACD,
∵在△DBH和△DCA中
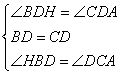 ,∴△DBH≌△DCA(ASA),∴BH=AC.
,∴△DBH≌△DCA(ASA),∴BH=AC.
(2)连接CG,
由(1)知,DB=CD,∵F为BC的中点,
∴DF垂直平分BC,∴BG=CG,
∵∠ABE=∠CBE,BE⊥AC,∴EC=EA,
在Rt△CGE中,由勾股定理得: ,
,
∵CE=AE,BG=CG,∴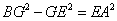 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,在直角坐标系中,点A、B的坐标分别为(2,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
(1)求过点A、B两点的直线解析式;
(2)在运动的过程中,当△ABC周长最小时,求点C的坐标;
(3)在运动的过程中,当△ABC是以AB为底的等腰三角形时,求点C的坐标.
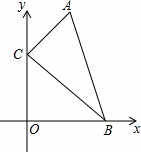
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
 (1)求证:△BCD≌△FCE;
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为 ,点C的坐标为
,点C的坐标为 ,点P为斜边OB上的一个动点,则PA+PC的最小值为…( )
,点P为斜边OB上的一个动点,则PA+PC的最小值为…( )
A.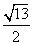 ;B.
;B. ; C.
; C. ;D.
;D. ;
;
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知函数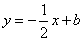 的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P
的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P 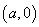 (其中
(其中 >2),过点P作x轴的垂线,分别交函数
>2),过点P作x轴的垂线,分别交函数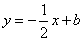 和
和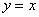 的图象于点C、D.
的图象于点C、D.
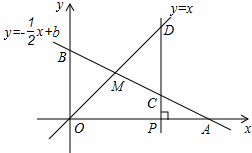 (1)求点A的坐标;
(1)求点A的坐标;
(2)若OB=CD,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )
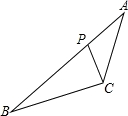
A.①②④ B.①③④ C.②③④ D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com