【题目】如图1四边形ABCD中,AB∥CD，AD=DC=CB=a，∠A=60°,取AB的中点A1 ， 连接A1C，再分别取A1C，BC的中点D1 ， C1连接D1C1 ． 得到四边形A1BC1D1 ， 如图2同样方法操作得到四边形A2BC2D2 ． 如图3……．如此进行下去，则四边形AnBCnDn的面积为 ．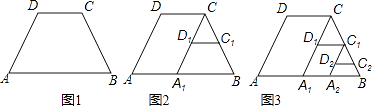 
科目：初中数学 来源： 题型：
【题目】【问题提出】
平面上，若点P与A、B、C三点中的任意两点均构成等腰三角形，则称点P是A、B、C三点的巧妙点．若A、B、C三点构成三角形，也称点P是△ABC的巧妙点．
【初步思考】
（1）如图①，在等边△ABC的内部和外部各作一个△ABC的巧妙点．（尺规作图，不写作法，保留作图痕迹）
（2）如图②，在△ABC中，AB＝AC，∠BAC＝36°，点D、E是△ABC的两个巧妙点，其中AD＝AB，AE＝AC，BD＝BC＝CE，连接DE，分别交AB、AC于点M、N．求证： DA2＝DB·DE．
【深入研究】
（3）在△ABC中，AB＝AC，若存在一点P，使PB＝BA，PA＝PC．点P可能为△ABC的巧妙点吗？若可能，请画出示意图，并直接写出∠BAC的度数；若不可能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD和正方形ECGF的边长分别为a和6，
(1) 写出表示阴影部分面积的代数式（结果要求化简）；
(2) 求
时，阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，菱形ABCD的顶点C的坐标为(-1，0)，点B的坐标为(0，2),点A在第二象限．直线y=- 
x+5与x轴、y轴分别交于点N、M将菱形ABCD沿x轴向右平移m个单位，当点D落在△MON的内部时 (不包括三角形的边)，则m的值可能是 ． (写出一个即可)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列事件中，是随机事件的是（ ）
A.两条直线被第三条直线所截，同位角相等
B.任意一个四边形的外角和等于360°
C.早上太阳从西方升起
D.平行四边形是中心对称图形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB与CD相交于点O，OD平分∠BOE，∠FOD=90°，问OF是∠AOE的平分线吗？请你补充完整小红的解答过程．
探究：
（1）当∠BOE=70°时，
∠BOD=∠DOE=
，
∠EOF=90°﹣∠DOE= °，
而∠AOF+∠FOD+∠BOD=180°，
所以∠AOF+∠BOD=180°﹣∠FOD=90°，
所以∠AOF=90°﹣∠BOD= °，
所以∠EOF=∠AOF，OF是∠AOE的平分线．
（2）参考上面（1）的解答过程，请你证明，当∠BOE为任意角度时，OF是∠AOE的平分线．
（3）直接写出与∠AOF互余的所有角．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和为（ ） 
A.2cm2
B.4cm2
C.6cm2
D.8cm2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利=售价﹣进价）
甲 | 乙 | |
进价（元/件） | 22 | 30 |
售价（元/件） | 29 | 40 |
（1）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（2）该超市第二次以第一次的进价又购进甲、乙两种商品．其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售．第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙种商品是按原价打几折销售？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
