
【题目】【问题提出】
平面上,若点P与A、B、C三点中的任意两点均构成等腰三角形,则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形,也称点P是△ABC的巧妙点.
【初步思考】
(1)如图①,在等边△ABC的内部和外部各作一个△ABC的巧妙点.(尺规作图,不写作法,保留作图痕迹)
(2)如图②,在△ABC中,AB=AC,∠BAC=36°,点D、E是△ABC的两个巧妙点,其中AD=AB,AE=AC,BD=BC=CE,连接DE,分别交AB、AC于点M、N.求证: DA2=DB·DE.

【深入研究】
(3)在△ABC中,AB=AC,若存在一点P,使PB=BA,PA=PC.点P可能为△ABC的巧妙点吗?若可能,请画出示意图,并直接写出∠BAC的度数;若不可能,请说明理由.
【答案】(1)作图见解析;
(2)证明见解析;
(3)点P能为△ABC的巧妙点,画出示意图见解析,画图见解析, ![]() ,
, ![]() ,
, ![]() 或
或![]()
【解析】(1)根据“巧妙点”的定义利用:点P在三角形的内部时,点P到△ABC的三个顶点的距离相等,所以点P是三角形的外心;点P在三角形的外部时,每条边的垂直平分线上的点只要能够使顶点这条边的两端点连接而成的三角形是等腰三角形即可;(2)先证明△ADB≌△ABC,△ACE≌△ABC,得到相等的角,再证明∠BMD=∠ABD,得到DB=DM.最后证明△DAM∽△DEA,得到![]() ,即DA=DMDE,由DM=DB,所以DA=DBDE.
,即DA=DMDE,由DM=DB,所以DA=DBDE.
(3)在△ABC中,AB=AC,若存在一点P,使PB=BA,PA=PC.点P能为△ABC的巧妙点,分别画出图形即可解答.
本题解析:(1) 如下图

(2)![]()
![]()
∴![]()
∴![]()
∴ ![]()
∴![]() ∴
∴![]() ,
, ![]()
又 ∵![]() ∴ DA2=DB·DE
∴ DA2=DB·DE
(3)第一种如图①或②(只需画出一个即可),![]()
第二种如图③,![]()
第三种如图④,![]()
第四种如图⑤,![]()



科目:初中数学 来源: 题型:
【题目】某宾馆客房有三人客房、双人客房,收费数据如下表:

为吸引游客,实行团体入住五折优惠措施,一个50人的旅游团优惠期间到该宾馆入住,住了若干间三人普通间客房和双人普通房间客房。若每间客房正好住满,且一天共花去住宿费1510元,则旅游团住了三人普通间和双人普通间客房各多少间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.
(1)写出∠AOC与∠BOD的大小关系并说明理由;
(2)若∠COF=34°26′,求∠BOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果商贩在批发市场按1.8元/千克批发了若干千克的苹果进城出售,为了方便,他带了一些零钱备用,他先按市场价出售一些后,又每千克下降0.5元将剩余的苹果降价售完,这时他手中的钱(含备用零钱)是450元.售出苹果x千克与他手中持有的钱数y元(含备用零钱)的关系如图所示,则这个水果商贩一共赚_____元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留在一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示x与y之间的关系,
请根据图象解决下列问题:
(1)甲乙两地之间的距离为_____千米;
(2)求快车和慢车的速度;
(3)点D表示_____点E表示_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板按图1所示的位置放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连接DC.

(1)请找出图2中与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图) 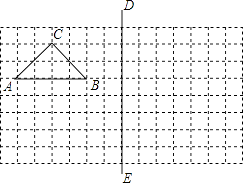
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB1+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1四边形ABCD中,AB∥CD,AD=DC=CB=a,∠A=60°,取AB的中点A1 , 连接A1C,再分别取A1C,BC的中点D1 , C1连接D1C1 . 得到四边形A1BC1D1 , 如图2同样方法操作得到四边形A2BC2D2 . 如图3…….如此进行下去,则四边形AnBCnDn的面积为 . 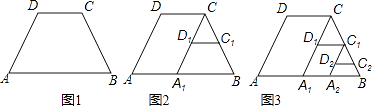
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com