
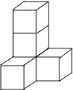
【题目】如图是由大小相同的棱长为![]() 的小正方体搭成的几何体,
的小正方体搭成的几何体,
![]() 请分别画出它的从正面、左面、上面看到的形状图.
请分别画出它的从正面、左面、上面看到的形状图.
![]() 摆成如图的形状后,表面积是多少?
摆成如图的形状后,表面积是多少?
【答案】(1)详见解析
(2)88.
【解析】
(1)观察图形可知,从正面看到的图形是2列,左边一列是3个正方形,右边一列是1个正方形在下面;从上面看到的图形是2行,后面一行是2个正方形,前面一行是1个正方形,在左边;从左面看到的图形和从正面看到的图形相同,据此即可画图.
(2)从上面和下面看,各有3个正方形面,从左面和右面看,各有4个正方形面,从前面和后面看,各有4个正方形面,一共有22个正方形面,一个正方形面的面积是2×2=4平方厘米,据此即可求出这个立体图形的表面积.
解:(1)如图所示: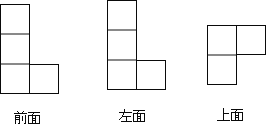
(2)(2×2)×(3×2+4×2+4×2)
=4×22
=88(平方厘米).
答:表面积是88平方厘米.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以直线
中,以直线![]() 向上的方向为新坐标系
向上的方向为新坐标系![]() 轴的正方向,过点
轴的正方向,过点![]() 作一与新
作一与新![]() 轴垂直的直线,垂足是点
轴垂直的直线,垂足是点![]() ,该直线向上的方向为新
,该直线向上的方向为新![]() 轴的正方向,由此建立新的坐标系
轴的正方向,由此建立新的坐标系![]() .
.
(1)新![]() 轴所在直线在
轴所在直线在![]() 坐标系中的表达式是什么?
坐标系中的表达式是什么?
(2)点![]() 在
在![]() 坐标系中坐标是
坐标系中坐标是![]() ,在坐标系
,在坐标系![]() 中的坐标是多少?
中的坐标是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.一次函数y=![]() x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.
x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.
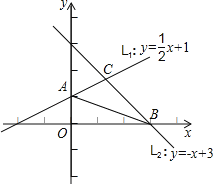
(1)求点A与点B的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
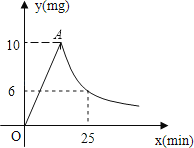
【题目】合肥三十八中为预防秋季疾病传播,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量![]() (毫克)与燃烧时间
(毫克)与燃烧时间![]() (分钟)之间的关系如图所示(即图中线段
(分钟)之间的关系如图所示(即图中线段![]() 和双曲线在
和双曲线在![]() 点及其右侧的部分),根据图象所示信息,解答下列问题:
点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)据测定,只有当空气中每立方米的含药量不低于![]() 毫克时,对预防才有作用,且至少持续作用
毫克时,对预防才有作用,且至少持续作用![]() 分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长为1,格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-5,5),(-2,3).

(1)请在图中的网格平面内画出平面直角坐标系xOy;
(2)请画出△ABC关于y轴对称的△A1B1C1,并写出顶点A1,B1,C1的坐标
(3)请在x轴上求作一点P,使△PB1C的周长最小.请标出点P的位置(保留作图痕迹,不需说明作图方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县盛产苹果,春节期问,一外地经销商安排![]() 辆汽年装运
辆汽年装运![]() 、
、![]() 、
、![]() 三种不同品质的苹果
三种不同品质的苹果![]() 吨到外地销售,按计划
吨到外地销售,按计划![]() 辆汽年都要装满且每辆汽车只能装同一种品质的苹果,每辆汽车的运载量及每吨苹果的获利如下表:
辆汽年都要装满且每辆汽车只能装同一种品质的苹果,每辆汽车的运载量及每吨苹果的获利如下表:
苹果品种 |
|
|
|
每辆汽车运载数 |
|
|
|
每吨获利(元) |
|
|
|
(1)设装运![]() 种苹果的车辆数为
种苹果的车辆数为![]() 辆,装运
辆,装运![]() 种苹果车辆数为
种苹果车辆数为![]() 辆,据上表提供的信息,求出
辆,据上表提供的信息,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)为了减少苹果的积压,县林业局制定出台了促进销售的优惠政策,在外地经销商原有获利不变情况下,政府对外地经销商按每吨![]() 元的标准实行运费补贴若
元的标准实行运费补贴若![]() 种苹果的车辆数
种苹果的车辆数![]() 满足
满足![]() .若要使该外地经销商所获利
.若要使该外地经销商所获利![]() (元)最大,应采用哪种车辆安排方案?并求出最大利润
(元)最大,应采用哪种车辆安排方案?并求出最大利润![]() (元)的最大值.
(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图像与x轴交于点
的图像与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)在坐标系中能否找到点![]() ,使得
,使得![]() 且
且![]() ?如果能,求出满足条件的点
?如果能,求出满足条件的点![]() 的坐标;如果不能,请说明理由.
的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
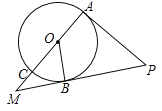
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程![]() (米)与时间
(米)与时间![]() (秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
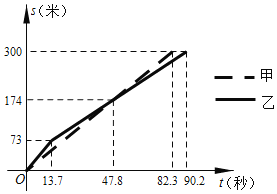
A. 乙队率先到达终点
B. 甲队比乙队多走了![]() 米
米
C. 在![]() 秒时,两队所走路程相等
秒时,两队所走路程相等
D. 从出发到![]() 秒的时间段内,乙队的速度慢
秒的时间段内,乙队的速度慢
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com