解:(1)①2(2x+1)-2(1+x)≥x+3,
4x+2-2-2x≥x+3,
4x-2x-x≥3-2+2,
x≥3,
在数轴上表示如下:

②

+1≥x,
x-1+2≥2x,
x-2x≥1-2,
-x≥-1,
x≤1,
在数轴上表示如下:

(2)①方程组可化为

,
①-②得,4y=28,
解得y=7,
把y=7代入①得,3x-7=8,
解得x=5,
所以,方程组的解是

;
②方程组可化为
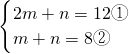
,
①-②得,m=4,
把m=4代入②得,4+n=8,
解得n=4,
所以,原方程组的解是
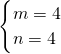
.
分析:(1)①先去括号,再移项,合并同类项,系数化为1,即可得解;
②先去分母,再移项,合并同类项,系数化为1即可得解;
(2)①先把方程组整理成一般形式,再跟x的系数相等,利用加减消元法求解即可;
②先去掉分母,整理成方程组的一般形式,再利用加减消元法求解即可.
点评:本题考查了不等式的性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.

 +1≥x
+1≥x
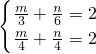 .
.
 +1≥x,
+1≥x,
 ,
, ;
;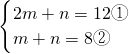 ,
,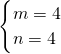 .
.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案