
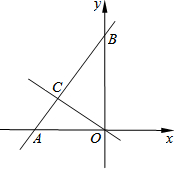
 如图,一次函数y=mx+2m+3的图象与y=-$\frac{1}{2}$x的图象交于点C,且点C的横坐标为-3,与x轴、y轴分别交于点A、点B.
如图,一次函数y=mx+2m+3的图象与y=-$\frac{1}{2}$x的图象交于点C,且点C的横坐标为-3,与x轴、y轴分别交于点A、点B.分析 (1)把点C的横坐标代入正比例函数解析式,求得点C的纵坐标,然后把点C的坐标代入一次函数解析式即可求得m的值,从而得到一次函数的解析式,则易求点A、B的坐标,然后根据勾股定理即可求得AB;
(2)由S△OCQ=$\frac{1}{4}$S△BAO得到OQ的长,即可求得Q点的坐标.
解答 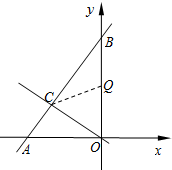 解:(1)∵点C在直线$y=-\frac{1}{2}x$上,点C的横坐标为-3,
解:(1)∵点C在直线$y=-\frac{1}{2}x$上,点C的横坐标为-3,
∴点C坐标为(-3,$\frac{3}{2}$),
又∵点C在直线y=mx+2m+3上,
∴$-3m+2m+3=\frac{3}{2}$,
∴$m=\frac{3}{2}$,
∴直线AB的函数表达式为$y=\frac{3}{2}x+6$,
令x=0,则y=6,令y=0,则$\frac{3}{2}$x+6=0,解得x=-4,
∴A(-4,0)、B(0,6),
∴AB=$\sqrt{{4}^{2}+{6}^{2}}$=$2\sqrt{13}$;
(2)∵${S_{△COQ}}=\frac{1}{4}{S_{△BAO}}$,
∴$\frac{3•OQ}{2}=\frac{1}{4}×\frac{4×6}{2}$,
∴OQ=2,
∴点Q坐标为(0,2).
点评 本题考查了两直线相交或平行问题、待定系数法求函数解析式、一次函数图象上点的坐标特征、勾股定理的应用、三角形的面积公式等知识,综合性较强,值得关注.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{3}{4}$ | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{13}{4}$ | -$\frac{7}{3}$ | -$\frac{3}{2}$ | -1 | -$\frac{3}{2}$ | -$\frac{13}{4}$ | $\frac{21}{4}$ | $\frac{7}{2}$ | 3 | $\frac{7}{2}$ | m | $\frac{21}{4}$ | … |
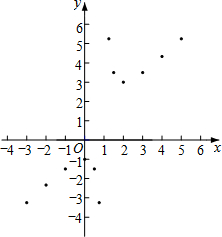
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上,使该图形能折成一个密封的正方形盒子.
如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上,使该图形能折成一个密封的正方形盒子.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
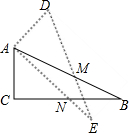 如图,在Rt△ABC中,∠C=90°,M为AB边上中点,将Rt△ABC绕点M旋转,使点C与点A重合得Rt△DEA,设AE交CB于点N.
如图,在Rt△ABC中,∠C=90°,M为AB边上中点,将Rt△ABC绕点M旋转,使点C与点A重合得Rt△DEA,设AE交CB于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com