
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC= ![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
【答案】
(1)证明:如图1
 ,
,
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)解:cos∠ABC= ![]() ,AB=12,得
,AB=12,得
OB=8.
由勾股定理,得
AO= ![]() =4
=4 ![]() .
.
由三角形的面积,得
S△AOB= ![]() ABOE=
ABOE= ![]() OBAO,
OBAO,
OE= ![]() =
= ![]() ,
,
半圆O所在圆的半径是 ![]()
【解析】本题考查了切线的判定与性质,利用切线的判定是解题关键,利用面积相等得出关于OE的长是解题关键.(1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;(2)根据余弦,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
(1)图1中a的值为;
(2)求统计的这组初赛成绩数据的平均数、众数和中位数;
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:AC2=APAB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程x2﹣3x+p=0(p≠0)的两个不相等的实数根分别为a和b,且a2﹣ab+b2=18,则 ![]() +
+ ![]() 的值是( )
的值是( )
A.3
B.﹣3
C.5
D.﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为 m(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() =
= ![]() ;
;
【结论应用】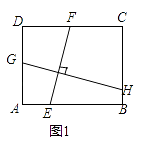
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 ![]() =
= ![]() ,则
,则 ![]() 的值为;
的值为;
【联系拓展】
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 ![]() 的值.
的值.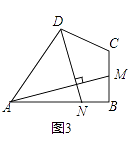
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x﹣1与反比例函数y= ![]() 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F. 
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com