
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
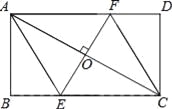
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
【答案】(1)证明过程见解析;(2)2![]()
【解析】试题分析:(1)由过AC的中点O作EF⊥AC,根据线段垂直平分线的性质,可得AF=CF,AE=CE,OA=OC,然后由四边形ABCD是矩形,易证得△AOF≌△COE,则可得AF=CE,继而证得结论;(2)由四边形ABCD是矩形,易求得CD的长,然后利用三角函数求得CF的长,继而求得答案.
试题解析:(1)∵O是AC的中点,且EF⊥AC, ∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形, ∴AD∥BC, ∴∠AFO=∠CEO, ∴△AOF≌△COE(AAS), ∴AF=CE,
∴AF=CF=CE=AE, ∴四边形AECF是菱形;
(2)∵四边形ABCD是矩形, ∴CD=AB=![]() , 在Rt△CDF中,cos∠DCF=
, 在Rt△CDF中,cos∠DCF=![]() ,∠DCF=30°,
,∠DCF=30°,
∴CF=![]() =2, ∵四边形AECF是菱形, ∴CE=CF=2, ∴四边形AECF是的面积为:ECAB=2
=2, ∵四边形AECF是菱形, ∴CE=CF=2, ∴四边形AECF是的面积为:ECAB=2![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】对于实数x,符号[x]表示不大于x的最大整数解,如:[π]=3,[6]=6,[-7.5]=-8.
(1)若[a]=-3,那么a的取值范围是 ______ ;
(2)若![]() =2,求满足条件的所有正整数a.
=2,求满足条件的所有正整数a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
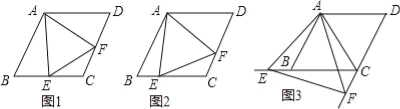
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
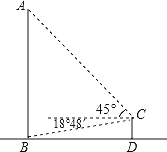
【题目】全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为 米(参考数据:tan78°12′≈4.8).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com