
【题目】如图,已知直线y=﹣x+4与反比例函数y=![]() 的图象相交于点A(﹣2,a),并且与x轴相交于点B.
的图象相交于点A(﹣2,a),并且与x轴相交于点B.
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积;
(4)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.

【答案】(1)6;(2)![]() ;(3)12;(4
;(3)12;(4![]() 或
或![]() .
.
【解析】
试题(1)直接利用待定系数法把A(﹣2,a)代入函数关系式y=﹣x+4中即可求出a的值;
(2)由(1)得到A点坐标后,设出反比例函数关系式,再把A点坐标代入反比例函数关系式,即可得到答案;
(3)根据题意画出图象,过A点作AD⊥x轴于D,根据A的坐标求出AD的长,再根据B点坐标求出OB的长,根据三角形面积公式即可算出△AOB的面积;
(4)求出直线与反比例函数的另一个交点,观察图象即可得到答案..
试题解析:(1)将A(﹣2,a)代入![]() 中,得:
中,得:![]() ,∴a=6;
,∴a=6;
(2)由(1)得:A(﹣2,6),将A(﹣2,6)代入![]() 中,得:
中,得:![]() ,∴
,∴![]() ,
,
∴反比例函数的表达式为:![]() ;
;
(3)如图:过A点作AD⊥x轴于D,∵A(﹣2,6),∴AD=6,
在直线![]() 中,令y=0,得x=4,∴B(4,0),∴OB=4,
中,令y=0,得x=4,∴B(4,0),∴OB=4,
∴△AOB的面积S=![]() OB×AD=12;
OB×AD=12;
(4)由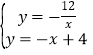 ,得:
,得:![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() .∴直线与反比例函数的交点为:(-2,6)和(6,-2),有图象可知,当
.∴直线与反比例函数的交点为:(-2,6)和(6,-2),有图象可知,当![]() 或
或![]() 时,一次函数的值大于反比例函数的值.
时,一次函数的值大于反比例函数的值.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
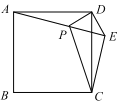
【题目】如图,在正方形![]() 外取一点
外取一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;④
;④![]() ;⑤
;⑤![]() 正方形
正方形![]() .其中正确的是( )
.其中正确的是( )
A.①②③④B.①②④⑤C.①③④D.①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
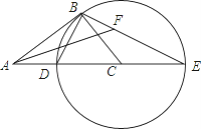
(1)求证:△ABD∽△AEB;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
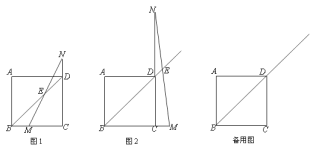
【题目】在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE=![]() BM;
BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是什么?;
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE=![]() ,且AF:FD=1:2时,求线段DG的长.
,且AF:FD=1:2时,求线段DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
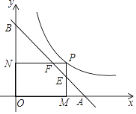
【题目】如图,P为反比例函数y= ![]() (x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=﹣x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AFBE的值为________.
(x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=﹣x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AFBE的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF

查看答案和解析>>
科目:初中数学 来源: 题型:
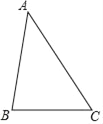
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC、AB交于点D、E.
(1)在图中作出AB的垂直平分线DE,并连接BD.
(2)证明:△ABC∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.
(1)分别求出当2≤x≤4时,三个函数:y=2x+1,y=![]() ,y=2(x﹣1)2+1的最大值和最小值;
,y=2(x﹣1)2+1的最大值和最小值;
(2)若y=![]() 的值不大于2,求符合条件的x的范围;
的值不大于2,求符合条件的x的范围;
(3)若y=![]() ,当a≤x≤2时既无最大值,又无最小值,求a的取值范围;
,当a≤x≤2时既无最大值,又无最小值,求a的取值范围;
(4)y=2(x﹣m)2+m﹣2,当2≤x≤4时有最小值为1,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com