
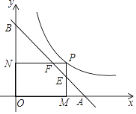
【题目】如图,P为反比例函数y= ![]() (x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=﹣x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AFBE的值为________.
(x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=﹣x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AFBE的值为________.
【答案】3
【解析】
如图,过F点作FH⊥x轴于H,过E点作EG⊥y轴于G,由直线y=-x+2与x轴、y轴分别交于A、B,可得△AOB是等腰直角三角形,继而可得△AFH也是等腰直角三角形,△BGE为等腰直角三角形,从而可得AF=![]() PM,BE=
PM,BE=![]() PN,可得AF×BE =2PMPN,由点P在y=
PN,可得AF×BE =2PMPN,由点P在y=![]() 上,可得PMPN=
上,可得PMPN=![]() ,继而可求得AF×BE=2PMPN=3,问题得以解决.
,继而可求得AF×BE=2PMPN=3,问题得以解决.
如图,过F点作FH⊥x轴于H,过E点作EG⊥y轴于G,则有FH=PM,PN=EG,
∵直线y=-x+2与x轴、y轴分别交于A、B,
∴A(2,0),B(0,2),
∴△AOB是等腰直角三角形,
∴△AFH也是等腰直角三角形,△BGE为等腰直角三角形,
∴AH=FH,BG=EG,
∴AF=![]() =
=![]() FH=
FH=![]() PM,BE=
PM,BE=![]() =
=![]() EG=
EG=![]() PN,
PN,
∴AF×BE=![]() PM×
PM×![]() PN=2PMPN,
PN=2PMPN,
∵y=![]() ,
,
∴PMPN=![]() ,
,
∴AF×BE=2PMPN=2×![]() =3,
=3,
故答案为:3.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(![]() +1)EH;③
+1)EH;③![]() =
=![]() . 其中正确的是( )
. 其中正确的是( )
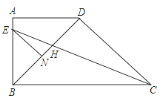
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在边BC上,连接AD,将线段AD绕点A逆时针旋转到AE,使得∠DAE=∠BAC,连接DE交AC于F,请写出图中一对相似的三角形:____(只要写出一对即可).
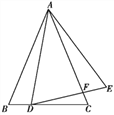
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办校级篮球赛,进入决赛的队伍有A、B、C、D,要从中选出两队打一场比赛.
(1)若已确定A打第一场,再从其余三队中随机选取一队,求恰好选中D队的概率.
(2)请用画树状图或列表法,求恰好选中B、C两队进行比赛的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+4与反比例函数y=![]() 的图象相交于点A(﹣2,a),并且与x轴相交于点B.
的图象相交于点A(﹣2,a),并且与x轴相交于点B.
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积;
(4)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
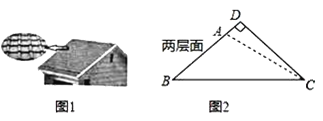
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)

(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张分别标有数字2,5,9的卡片,它们的背面都相同.现将它们背面朝上,从中任意抽出一张卡片,不放回,再从剩余的两张卡片里任意抽出一张.
(1)请用树状图或列表法表示出所有可能的结果.
(2)求两张卡片的数字之和为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com