
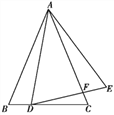
【题目】如图,在△ABC中,AB=AC,点D在边BC上,连接AD,将线段AD绕点A逆时针旋转到AE,使得∠DAE=∠BAC,连接DE交AC于F,请写出图中一对相似的三角形:____(只要写出一对即可).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了解宣城市市民“绿色出行”方式的情况,我校数学兴趣小组以问卷调查的形式,随机调查了宣城市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 |
|
|
|
|
|
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
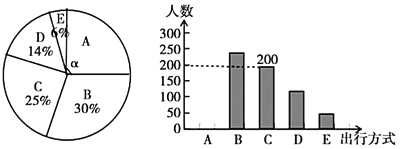
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有______人,其中选择![]() 类的人数有______人;
类的人数有______人;
(2)在扇形统计图中,求![]() 类对应扇形圆心角
类对应扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)宣城市约有人口280万人,若将![]() 、
、![]() 、
、![]() 这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
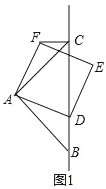
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一个动点,(点D不要B,C重合),以AD为边在AD的上边作正方形ADEF,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①BC与CF的位置关系为_____;②AC、CD、CF之间的数量关系为_____.
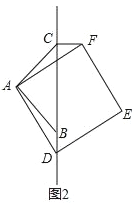
(2)如图2,当点D在线段CB的延长线上时,以上①、②关系是否成立?若成立去,请给出证明;若不成立,请写出正确的结论,并说明理由.
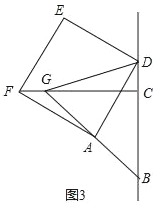
(3)如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GD,若AB=2![]() ,CD=
,CD=![]() BC,求出DG的长.
BC,求出DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A,B两点,AB=18,原点O是线段AB上的一点,OA=2OB.
(1)求出A,B两点所表示的数;
(2)若点C是线段AO上一点,且满足 AC=CO+CB,求C点所表示的数;
(3)若点E以3个单位长度/秒的速度从点A沿数轴向点B方向匀速运动,同时点F以1个单位长度/秒的速度从点B沿数轴向右匀速运动,并设运动时间为t秒,问t为多少时,E、F两点重合.并求出此时数轴上所表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条不完整的数轴上一动点![]() 向左移动5个单位长度到达点
向左移动5个单位长度到达点![]() ,再向右移动9个单位长度到达点
,再向右移动9个单位长度到达点![]() .
.

(1)①若点![]() 表示的数为0,则点
表示的数为0,则点![]() 、点
、点![]() 表示的数分别为: 、 ;
表示的数分别为: 、 ;
②若点![]() 表示的数为1,则点
表示的数为1,则点![]() 、点
、点![]() 表示的数分别为: 、 ;
表示的数分别为: 、 ;
(2)如果点![]() 、
、![]() 表示的数互为相反数,求点
表示的数互为相反数,求点![]() 表示的数.
表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知△ABC和△DEF的顶点分别为A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).
中,已知△ABC和△DEF的顶点分别为A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).
按下列要求画图:以点O为位似中心,将△ABC向y轴左侧按比例尺2:1放大得△ABC的位似图形△A1B1C1,并解决下列问题:
(1)顶点A1的坐标为 ,B1的坐标为 ,C1的坐标为 ;
(2)请你利用旋转、平移两种变换,使△A1B1C1通过变换后得到△A2B2C2,且△A2B2C2恰与△DEF拼接成一个平行四边形(非正方形),写出符合要求的变换过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:计算![]() (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算![]() .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() .
.

探究二:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() ,
,
两边同除以2,得![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ﹣
﹣![]() .
.

探究三:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式:_________,
所以,![]() +
+![]() +
+![]() +…+
+…+![]() =________.
=________.
拓广应用:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com