
【题目】为了解宣城市市民“绿色出行”方式的情况,我校数学兴趣小组以问卷调查的形式,随机调查了宣城市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 |
|
|
|
|
|
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
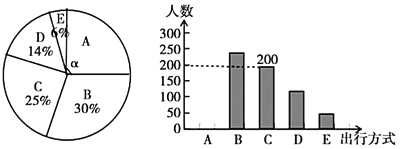
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有______人,其中选择![]() 类的人数有______人;
类的人数有______人;
(2)在扇形统计图中,求![]() 类对应扇形圆心角
类对应扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)宣城市约有人口280万人,若将![]() 、
、![]() 、
、![]() 这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D为边BC上一点,E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,连结BF.
(1)求证:四边形ADBF是平行四边形;
(2)当D为边BC的中点,且BC=2AC时,求证:四边形ACDF为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上.
上.
(1)若点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)连接![]() ,若点
,若点![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,且交直线
,且交直线![]() 于点
于点![]() .若
.若![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,点M、N分别是AD、BC的中点,如果BC=10,AD=4,那么MN的长是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() 在数轴上,数轴上点
在数轴上,数轴上点![]() 表示的数为
表示的数为![]() ,正方形
,正方形![]() 的面积为16.
的面积为16.
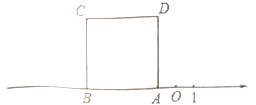
(1)数轴上点![]() 表示的数为__________;
表示的数为__________;
(2)将正方形![]() 沿数轴水平移动,移动后的正方形记为
沿数轴水平移动,移动后的正方形记为![]() ,移动后的正方形
,移动后的正方形![]() 与原正方形
与原正方形![]() 重叠部分的面积记为
重叠部分的面积记为![]() .当
.当![]() 时,画出图形,并求出数轴上点
时,画出图形,并求出数轴上点![]() 表示的数;
表示的数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购进A,B两种树木共100棵进行校园绿化,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A,B两种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借助一副三角板,可以得到一些平面图形
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.
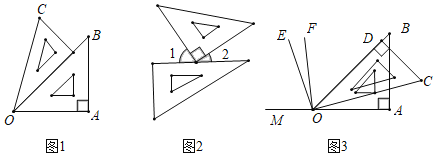
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在边BC上,连接AD,将线段AD绕点A逆时针旋转到AE,使得∠DAE=∠BAC,连接DE交AC于F,请写出图中一对相似的三角形:____(只要写出一对即可).
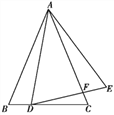
查看答案和解析>>
科目:初中数学 来源: 题型:
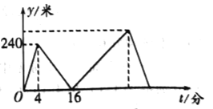
【题目】小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行![]() 米,先到终点的人原地休息.已知小莹先出发
米,先到终点的人原地休息.已知小莹先出发![]() 分钟,在整个步行过程中,两人的距离
分钟,在整个步行过程中,两人的距离![]() (米)与小莹出发的时间
(米)与小莹出发的时间![]() (分)之间的关系如图所示,下列结论:①小莹的步行速度为
(分)之间的关系如图所示,下列结论:①小莹的步行速度为![]() 米/分;②小亮用
米/分;②小亮用![]() 分钟追上小莹;③小亮走完全程用了
分钟追上小莹;③小亮走完全程用了![]() 分钟;④小亮到达终点时,小莹离终点还有
分钟;④小亮到达终点时,小莹离终点还有![]() 米。其中正确的结论有( )
米。其中正确的结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com