
【题目】某校计划购进A,B两种树木共100棵进行校园绿化,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A,B两种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
【答案】(1)A种树每棵100元,B种树每棵80元;(2)当购买A种树木75棵,B种树木25棵时,所需费用最少,最少为8550元.
【解析】分析:(1)、设A种树每棵x元,B种树每棵y元,根据题意列出二元一次方程组,从而得出答案;(2)、设购买A种树木为a棵,根据题意列出y与a的函数关系式,根据a的取值范围得出最值.
详解:(1)设A种树每棵x元,B种树每棵y元,
依题意得:![]() ,解得
,解得![]() .
.
答:A种树每棵100元,B种树每棵80元;
(2)设购买A种树木为a棵,则购买B种树木为(100﹣a)棵,则a≥3(100﹣a),
解得a≥75. 设实际付款总金额是y元,则
y=0.9[100a+80(100﹣a)],即y=18a+7200.
∵18>0,y随a的增大而增大, ∴当a=75时,y最小.
即当a=75时,y最小值=18×75+7200=8550(元).
答:当购买A种树木75棵,B种树木25棵时,所需费用最少,最少为8550元


科目:初中数学 来源: 题型:
【题目】已知,如图![]() ,
,![]() 分别为数轴上的两点,点
分别为数轴上的两点,点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数为80.
对应的数为80.

(1)请直接写出![]() 的中点
的中点![]() 对应的数.
对应的数.
(2)现在有一只电子蚂蚁![]() 从
从![]() 点出发,以2个单位/秒的速度向左运动,同时另一只电子蚂蚁
点出发,以2个单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以3个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
点出发,以3个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇.请解答下面问题:
点相遇.请解答下面问题:
①试求出点![]() 在数轴上所对应的数;
在数轴上所对应的数;
②何时两只电子蚂蚁在数轴上相距15个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解宣城市市民“绿色出行”方式的情况,我校数学兴趣小组以问卷调查的形式,随机调查了宣城市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 |
|
|
|
|
|
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
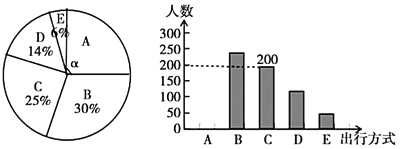
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有______人,其中选择![]() 类的人数有______人;
类的人数有______人;
(2)在扇形统计图中,求![]() 类对应扇形圆心角
类对应扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)宣城市约有人口280万人,若将![]() 、
、![]() 、
、![]() 这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上,且B(0,4).
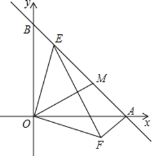
(1)求线段AB的长;
(2)若点E在线段AB上,OE⊥OF,且OE=OF,求AE+AF的值;
(3)在(2)的条件下,过O作OM⊥EF,交AB于M,试确定线段BE、EM、AM之间的数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一个动点,(点D不要B,C重合),以AD为边在AD的上边作正方形ADEF,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①BC与CF的位置关系为_____;②AC、CD、CF之间的数量关系为_____.
(2)如图2,当点D在线段CB的延长线上时,以上①、②关系是否成立?若成立去,请给出证明;若不成立,请写出正确的结论,并说明理由.
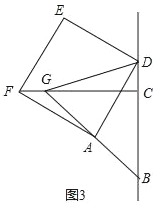
(3)如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GD,若AB=2![]() ,CD=
,CD=![]() BC,求出DG的长.
BC,求出DG的长.
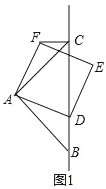
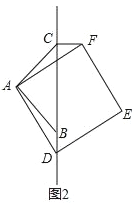
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() 的图象与x轴交于点A、
的图象与x轴交于点A、![]() ,顶点为
,顶点为![]()
![]() 求该二次函数的解析式;
求该二次函数的解析式;
![]() 如图,过A、C两点作直线,并将线段AC沿该直线向上平移,记点A、C分别平移到点D、E处
如图,过A、C两点作直线,并将线段AC沿该直线向上平移,记点A、C分别平移到点D、E处![]() 若点F在这个二次函数的图象上,且
若点F在这个二次函数的图象上,且![]() 是以EF为斜边的等腰直角三角形,求点F的坐标;
是以EF为斜边的等腰直角三角形,求点F的坐标;
![]() 试确定实数p,q的值,使得当
试确定实数p,q的值,使得当![]() 时,
时,![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com