
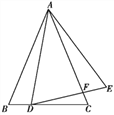
����Ŀ����ͼ���ڡ�ABC�У���BAC=90�㣬AB=AC����DΪֱ��BC��һ�����㣬����D��ҪB��C�غϣ�����ADΪ����AD���ϱ���������ADEF������CF��
��1���۲���룺��ͼ1������D���߶�BC��ʱ����BC��CF��λ�ù�ϵΪ_____����AC��CD��CF֮���������ϵΪ_____��
��2����ͼ2������D���߶�CB���ӳ�����ʱ�����Ϣ����ڹ�ϵ�Ƿ������������ȥ�������֤����������������д����ȷ�Ľ��ۣ���˵�����ɣ�
��3����ͼ3������D���߶�BC���ӳ�����ʱ���ӳ�BA��CF�ڵ�G������GD����AB=2![]() ��CD=
��CD=![]() BC�����DG�ij���
BC�����DG�ij���
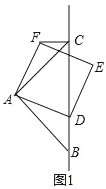
���𰸡� BC��CF CF+CD=![]() AC
AC
����������������1����֤����BAD=��CAF����SAS֤����BAD�ա�CAF���ó���ACF=��ABD=45�㣬֤����ACF+��ACB=90�㣬���ɵó����ۣ�����ȫ�������ε����ʵó�BD=CF��֤��CF=BC-CD���ɣ�(2)����֤����BAD=��CAF����SAS֤����BAD�ա�CAF���ó���ACF=��ABD=180��-45��=135�㣬֤����ACB+��FCB=135�㣬�ó���FCB=90�㣬���ɵó����ۣ�
����ȫ�������ε����ʵó�BD=CF��֤��CF=CD-BC���ɣ�(3)����SAS֤����BAD�ա�CAF���ó���ACF=��ABD=45�㣬֤����FCB=��ACF+��ACB=90�㣬�ó�CF��BC����Rt��ABC�У��ɹ��ɶ����ó�AC=AB=2![]() ����Rt��AGC�У��ó�CG=
����Rt��AGC�У��ó�CG=![]() AC=4��ͬ��BC=4��CD=
AC=4��ͬ��BC=4��CD=![]() BC=1����Rt��DCG�У��ɹ��ɶ����������DG�ij���
BC=1����Rt��DCG�У��ɹ��ɶ����������DG�ij���
��⣺��1���١ߡ�BAC=90�㣬AB=AC�����ABC=��ACB=45�㣬���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬�ߡ�BAC=��BAD+��DAC=90�㣬��DAF=��CAF+��DAC=90�㣬
���BAD=��CAF���ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF��
���BAD�ա�CAF��SAS�������ACF=��ABD=45�㣬���ACF+��ACB=90�㣬���BCF=90�㣬
��BC��CF��
�ڡߡ�BAD�ա�CAF����BD=CF����BD+CD=BC����CF+CD=BC���֡�Rt��ABC�У�BC=![]() AC��
AC��
��CF+CD=![]() AC��
AC��
��2���ٳ������ڲ���������ȷ�Ľ���ΪCD��CF=![]() AC��
AC��
���ɣ��١ߡ�BAC=90�㣬AB=AC�����ABC=��ACB=45�㣬���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬�ߡ�BAC=��BAF+��FAC=90�㣬��DAF=��BAF+��DAB=90�㣬
���BAD=��CAF���ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF��
AB=AC����BAD=��CAF��AD=AF�� ���BAD�ա�CAF��SAS����
���ACF=��ABD=180�㩁45��=135�㣬���ACB+��FCB=135�㣬 ���FCB=90�㣬 ��BC��CF��
�ڡߡ�BAD�ա�CAF����BD=CF����CD��BD=BC��CD��CF=BC��
�֡�Rt��ABC�У�BC=![]() AC�� ��CD��CF=
AC�� ��CD��CF=![]() AC��
AC��
��3��������ã���BAC=��FAD=90�㣬 ���BAD=��CAF��
�ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF�����BAD�ա�CAF��SAS����
���ACF=��ABD=45�㣬���FCB=��ACF+��ACB=45��+45��=90�㣬��CF��BC��
��Rt��ABC�У�AC=AB=2![]() ��BC=4����Rt��AGC�У��ߡ�ACF=45�㣬
��BC=4����Rt��AGC�У��ߡ�ACF=45�㣬
��CG=![]() AC=
AC=![]() ��2
��2![]() =4�� ��CD=
=4�� ��CD=![]() BC=
BC=![]() ��4=1��
��4=1��
����Rt��DCG��DG=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A����O��һ��OA�ϣ���Ҫ��ͼ����գ�

��1������A��ֱ��AB ��OA������O����һ���ཻ�ڵ�B��
��2������A��OB�Ĵ��߶�AC������Ϊ��C��
��3������C��ֱ��CD��OA ����ֱ��AB�ڵ�D��
��4����CDB= ����
��5�����OA=8��AB=6��OB=10�����A��ֱ��OB�ľ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������ABCD��,AD��BC,��C=36��,��B=54������M��N�ֱ���AD��BC���е㣬���BC=10��AD=4����ôMN�ij���___.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ƻ�����A��B������ľ��100�ý���У�̻������г����飺����A����ľ2�ã�B����ľ5�ã�����600Ԫ������A����ľ3�ã�B����ľ1�ã�����380Ԫ��
��1����A��B������ľÿ�ø�����Ԫ��
��2������Ҫ������A����ľ������������B����ľ������3����ʵ�ʸ����ܽ��г��۾����Żݣ������һ�ֹ�����ľ�ķ�����ʹʵ������������ʡ���������ʡ�ķ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ǰ壬���Եõ�һЩƽ��ͼ��
��1����ͼ1����AOC���� ���ȣ�������OA��OB��OC��ɵ�����С��ƽ�ǵĺ��Ƕ��ٶȣ�
��2����ͼ2����1�Ķ����ȡ�2������3������30�������2�Ķ�����
��3������ͼ3�������ӳ�����OA��M��OEƽ�֡�BOM��OFƽ�֡�COM���밴���ⲹȫͼ��3�����������EOF�Ķ�����
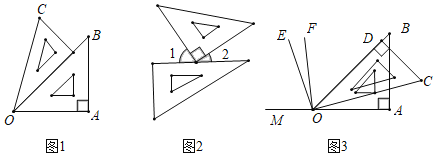
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У������е�ÿ��С�����α߳���1������ABC�Ķ�����ڸ���ϣ�����������ֱ������ϵ�н���������⣺

��1��������ABC�Ƶ�A��ʱ����ת90��ġ�A1B1C1��������ABC����ԭ��O�����ĶԳƵġ�A2B2C2��
��2����B1������Ϊ__________����C2������Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC��,AB=AC,��D�ڱ�BC��,����AD,���߶�AD�Ƶ�A��ʱ����ת��AE,ʹ�á�DAE=��BAC,����DE��AC��F,��д��ͼ��һ�����Ƶ�������:____(ֻҪд��һ�Լ���).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ļ����϶���һ��������![]() ��
��![]() ��
��![]() �����㼶����ڼӼ��˳����㣬��
�����㼶����ڼӼ��˳����㣬��![]() ������˳��Ҫ������
������˳��Ҫ������![]() ���㣬�Ը��������ش��������⣮
���㣬�Ը��������ش��������⣮
��1�����㣺![]() ��
��
��2����![]() ����
����![]() ��
��
��3���������ϣ���![]() ��λ������ͼ��ʾ���Ի���
��λ������ͼ��ʾ���Ի���![]() ��
��
![]()
��4����ͼ��ʾ���������ϣ���![]() �ֱ���1����λÿ����ٶȴӱ�ʾ��-1��3�ĵ㿪ʼ�˶�����
�ֱ���1����λÿ����ٶȴӱ�ʾ��-1��3�ĵ㿪ʼ�˶�����![]() ���������˶�����
���������˶�����![]() �����˶���
�����˶���![]() ����
����![]() �ֱ��˶�����ʾ��
�ֱ��˶�����ʾ��![]() ��
��![]() �ĵ����ڵ�λ�ã���
�ĵ����ڵ�λ�ã���![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CDΪ��O��ֱ������AE��CD������BE��CD�ڵ�F������E��ֱ��EP��CD���ӳ��߽��ڵ�P��ʹ��PED=��C��
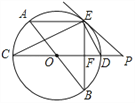
��1����֤��PE�ǡ�O�����ߣ�
��2����֤��EDƽ�֡�BEP.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com