
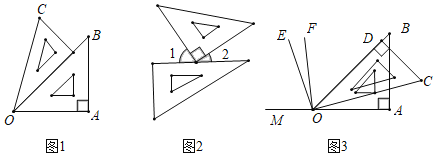
【题目】借助一副三角板,可以得到一些平面图形
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.
【答案】(1)75°,150°;(2)15°;(3)15°.
【解析】
(1)根据三角板的特殊性角的度数,求出∠AOC即可,把∠AOC、∠BOC、∠AOB相加即可求出射线OA,OB,OC组成的所有小于平角的和;
(2)依题意设∠2=x,列等式,解方程求出即可;
(3)依据题意求出∠BOM,∠COM,再根据角平分线的性质得出∠MOE,∠MOF,即可求出∠EOF.
解:(1)∵∠BOC=30°,∠AOB=45°,
∴∠AOC=75°,
∴∠AOC+∠BOC+∠AOB=150°;
答:由射线OA,OB,OC组成的所有小于平角的和是150°;
故答案为:75;
(2)设∠2=x,则∠1=3x+30°,
∵∠1+∠2=90°,
∴x+3x+30°=90°,
∴x=15°,
∴∠2=15°,
答:∠2的度数是15°;
(3)如图所示,∵∠BOM=180°﹣45°=135°,∠COM=180°﹣15°=165°,
∵OE为∠BOM的平分线,OF为∠COM的平分线,
∴∠MOF=![]() ∠COM=82.5°,∠MOE=
∠COM=82.5°,∠MOE=![]() ∠MOB=67.5°,
∠MOB=67.5°,
∴∠EOF=∠MOF﹣∠MOE=15°.


科目:初中数学 来源: 题型:
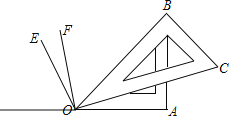
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
(1)∠PBD的度数为 ,点D的坐标为 (用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
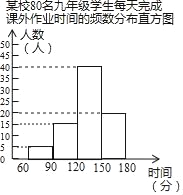
【题目】为了解九年级课业负担情况,某校随机抽取80名九年级学生进行问卷调查,在整理并汇总这80张有效问卷的数据时发现,每天完成课外作业时间,最长不超过180分钟,最短不少于60分钟,并将调查结果绘制成如图所示的频数分布直方图.
(1)被调查的80名学生每天完成课外作业时间的中位数在_____组(填时间范围).
(2)该校九年级共有800名学生,估计大约有_____名学生每天完成课外作业时间在120分钟以上(包括120分钟)
查看答案和解析>>
科目:初中数学 来源: 题型:
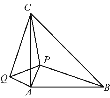
【题目】如图,在等腰△ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC=![]() ,将△APB绕点A逆时针旋转后与△AQC重合.求:
,将△APB绕点A逆时针旋转后与△AQC重合.求:
(1)线段PQ的长;
(2)∠APC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
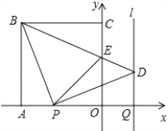
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
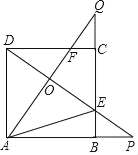
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于方程![]() =1,某同学解法如下:
=1,某同学解法如下:
解:方程两边同乘6,得3x﹣2(x﹣1)=1 ①
去括号,得3x﹣2x﹣2=1 ②
合并同类项,得x﹣2=1 ③
解得x=3 ④
∴原方程的解为x=3 ⑤
(1)上述解答过程中的错误步骤有 (填序号);
(2)请写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
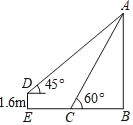
【题目】小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.
(1)填空:AD_____AC(填“>”,“<”,“=”).
(2)求旗杆AB的高度.
(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果精确到0.1m).
≈1.73,结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
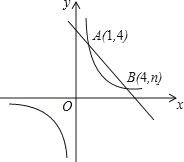
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com