
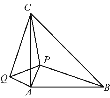
【题目】如图,在等腰△ABC中,∠CAB=90°,P是△ABC内一点,PA=1,PB=3,PC=![]() ,将△APB绕点A逆时针旋转后与△AQC重合.求:
,将△APB绕点A逆时针旋转后与△AQC重合.求:
(1)线段PQ的长;
(2)∠APC的度数.
【答案】(1)![]() ;(2)135°
;(2)135°
【解析】
(1)由性质性质得,AQ=AP=1,∠QAP=∠CAB=90°,由勾股定理得,PQ=![]() .
.
(2)由∠QAP=90°,AQ=AP,得∠APQ=45°,根据勾股定理逆定理得∠CPQ=90°,所以,∠APC=∠CPQ+∠APQ=135°.
解:(1)∵△APB绕点A旋转与△AQC重合,
∴AQ=AP=1,∠QAP=∠CAB=90°,
∴在Rt△APQ中,PQ=![]() .
.
(2)∵∠QAP=90°,AQ=AP,
∴∠APQ=45°.
∵△APB绕点A旋转与△AQC重合,
∴CQ=BP=3.
在△CPQ中,PQ=![]() ,CQ=3,CP=
,CQ=3,CP=![]() ,
,
∴CP2+PQ2=CQ2,
∴∠CPQ=90°,
∴∠APC=∠CPQ+∠APQ=135°.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…,依次规律,第9个图形圆的个数为( )
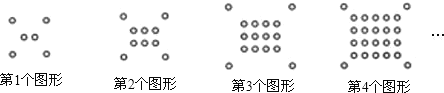
A.94B.85C.84D.76
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校以班为单位举行了“书法、版画、独唱、独舞”四项预选赛,参赛总人数达480人之多,下面是七年级一班此次参赛人数的两幅不完整的统计图,请结合图中信息解答下列问题:
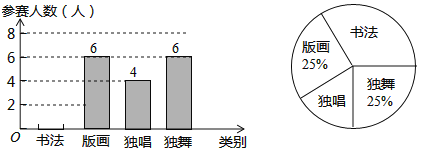
(1)求该校七年一班此次预选赛的总人数;
(2)补全条形统计图,并求出书法所在扇形圆心角的度数;
(3)若此次预选赛一班共有2人获奖,请估算本次比赛全学年约有多少名学生获奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
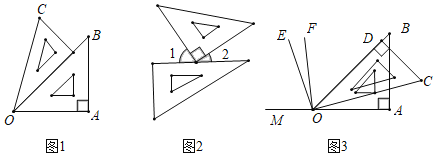
【题目】借助一副三角板,可以得到一些平面图形
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点![]() 、
、![]() 表示的数分别为
表示的数分别为![]() 、3.
、3.![]() 为数轴上一动点,其表示的数为
为数轴上一动点,其表示的数为![]() .
.
![]()
(1)若![]() 到
到![]() 、
、![]() 的距离相等,则
的距离相等,则![]() ______;
______;
(2)是否存在点![]() ,使
,使![]() ?若存在,写出
?若存在,写出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,沿数轴正方向分别以2个单位/秒、1个单位/秒的速度运动,则经过多长时间,
同时出发,沿数轴正方向分别以2个单位/秒、1个单位/秒的速度运动,则经过多长时间,![]() 、
、![]() 两点相距1个单位长度?
两点相距1个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)a= ,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com