
【题目】对于方程![]() =1,某同学解法如下:
=1,某同学解法如下:
解:方程两边同乘6,得3x﹣2(x﹣1)=1 ①
去括号,得3x﹣2x﹣2=1 ②
合并同类项,得x﹣2=1 ③
解得x=3 ④
∴原方程的解为x=3 ⑤
(1)上述解答过程中的错误步骤有 (填序号);
(2)请写出正确的解答过程.
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 点作射线
点作射线![]() ,使
,使![]() ,将一直角三角板的直角项点放在点
,将一直角三角板的直角项点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.
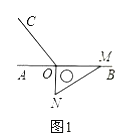
![]() 如图2,将图1中的三角板绕点
如图2,将图1中的三角板绕点![]() 逆时针旋转,使边
逆时针旋转,使边![]() 在
在![]() 的内部,且
的内部,且![]() 恰好平分
恰好平分![]() .此时
.此时![]() __ 度;
__ 度;
![]() 如图3,继续将图2中的三角板绕点
如图3,继续将图2中的三角板绕点![]() 按逆时针方向旋转,使得
按逆时针方向旋转,使得![]() 在
在![]() 的内部.试探究
的内部.试探究![]() 与
与![]() 之间满足什么等量关系,并说明理由;
之间满足什么等量关系,并说明理由;
![]() 将图1中的三角板绕点
将图1中的三角板绕点![]() 按每秒
按每秒![]() 的速度沿逆时针方向旋转一周,在旋转的过程中,若第
的速度沿逆时针方向旋转一周,在旋转的过程中,若第![]() 秒时,
秒时,![]() 三条射线恰好构成相等的角,则
三条射线恰好构成相等的角,则![]() 的值为__ (直接写出结果).
的值为__ (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
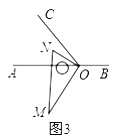
【题目】借助一副三角板,可以得到一些平面图形
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点![]() 、
、![]() 表示的数分别为
表示的数分别为![]() 、3.
、3.![]() 为数轴上一动点,其表示的数为
为数轴上一动点,其表示的数为![]() .
.
![]()
(1)若![]() 到
到![]() 、
、![]() 的距离相等,则
的距离相等,则![]() ______;
______;
(2)是否存在点![]() ,使
,使![]() ?若存在,写出
?若存在,写出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,沿数轴正方向分别以2个单位/秒、1个单位/秒的速度运动,则经过多长时间,
同时出发,沿数轴正方向分别以2个单位/秒、1个单位/秒的速度运动,则经过多长时间,![]() 、
、![]() 两点相距1个单位长度?
两点相距1个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com