
����Ŀ����ѧ���⣺����![]() ������m��n��������������m��2��n��1����
������m��n��������������m��2��n��1����
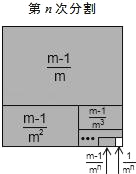
̽�����⣺Ϊ����������ѧ���⣬�����������ν�ϵ�˼�뷽����ͨ�����ϵطָ�һ�����Ϊ1�������Σ���������ϵ�ͼ���ͼ������ؽ������������ȡһ���������⻯�IJ���������̽����
̽��һ������![]() ��
��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ![]() ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ![]() +
+![]() ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ȷ֣�������Ӱ���ֵ����֮��Ϊ![]() +
+![]() +
+![]() +��+
+��+![]() �����հײ��ֵ������
�����հײ��ֵ������![]() ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��![]() +
+![]() +
+![]() +��+
+��+![]() =1��
=1��![]() ��
��

̽����������![]() +
+![]() +
+![]() +��+
+��+![]() ��
��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ![]() ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ![]() +
+![]() ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ����������ȷ֣�������Ӱ���ֵ����֮��Ϊ![]() +
+![]() +
+![]() +��+
+��+![]() �����հײ��ֵ������
�����հײ��ֵ������![]() ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��![]() +
+![]() +
+![]() +��+
+��+![]() =1��
=1��![]() ��
��
����ͬ����2����![]() +
+![]() +
+![]() +��+
+��+![]() =
=![]() ��
��![]() ��
��

̽����������![]() +
+![]() +
+![]() +��+
+��+![]() ��
��
����������������ֻ������n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ�����������д��̽�����̣�

������⣺����![]() +
+![]() +
+![]() +��+
+��+![]() ��
��
��ֻ�軭����n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ��������������������գ�
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��_________��
���ԣ�![]() +
+![]() +
+![]() +��+
+��+![]() =________��
=________��
�ع�Ӧ�ã�����![]() +
+![]() +
+![]() +��+
+��+![]() ��
��
���𰸡�![]()
![]()
��������
̽����������̽�����ķָ�����ν��зָȻ���ʾ����Ӱ���ֵ�������ٳ���3���ɣ�
������⣺����̽�����ķָ�����ηָȻ���ʾ����Ӱ���ֵ���������ٳ��ԣ�m-1�����ɵý⣻
�ع�Ӧ�ã��Ȱ�ÿһ�������ֳ�1��ȥһ��������Ȼ��Ӧ�ù�ʽ���м��㼴�ɵý⣮
̽��������1�ηָ�������ε�����ĵȷ֣�

������Ӱ���ֵ����Ϊ![]() ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ĵȷ֣�
��Ӱ���ֵ����֮��Ϊ![]() ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ĵȷ֣�
����
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ��������ĵȷ֣�
������Ӱ���ֵ����֮��Ϊ��![]() ��
��
���Ŀհײ��ֵ������![]() ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ��![]() =1��
=1��![]() ��
��
����ͬ����3����![]() =
=![]() ��
��
������⣺![]() =1��
=1��![]() ��
��
![]() =
=![]() ��
��
�ʴ�Ϊ��![]() =1��
=1��![]() ��
��![]() ��
��
�ع�Ӧ�ã�![]() ��
��
=1��![]() +1��
+1��![]() +1��
+1��![]() +��+1��
+��+1��![]() ��
��
=n����![]() +
+![]() +
+![]() +��+
+��+![]() ����
����
=n����![]() ��
��![]() ����
����
=n��![]() +
+![]() ��
��


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
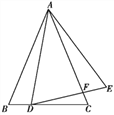
����Ŀ����ͼ,�ڡ�ABC��,AB=AC,��D�ڱ�BC��,����AD,���߶�AD�Ƶ�A��ʱ����ת��AE,ʹ�á�DAE=��BAC,����DE��AC��F,��д��ͼ��һ�����Ƶ�������:____(ֻҪд��һ�Լ���).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
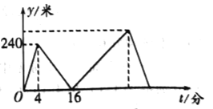
����Ŀ��СӨ��С���ڱ�ֱ�Ĺ�·��ͬ��㡢ͬ�յ㡢ͬ�������ٲ���![]() �ף��ȵ��յ����ԭ����Ϣ.��֪СӨ�ȳ���
�ף��ȵ��յ����ԭ����Ϣ.��֪СӨ�ȳ���![]() ���ӣ����������й����У����˵ľ���
���ӣ����������й����У����˵ľ���![]() ���ף���СӨ������ʱ��
���ף���СӨ������ʱ��![]() ���֣�֮��Ĺ�ϵ��ͼ��ʾ�����н��ۣ���СӨ�IJ����ٶ�Ϊ
���֣�֮��Ĺ�ϵ��ͼ��ʾ�����н��ۣ���СӨ�IJ����ٶ�Ϊ![]() ��/�֣���С����
��/�֣���С����![]() ������СӨ����С������ȫ������
������СӨ����С������ȫ������![]() ���ӣ���С�������յ�ʱ��СӨ���յ㻹��
���ӣ���С�������յ�ʱ��СӨ���յ㻹��![]() �ס�������ȷ�Ľ����У� ��
�ס�������ȷ�Ľ����У� ��
A. ![]() ��B.
��B. ![]() ��C.
��C. ![]() ��D.
��D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CDΪ��O��ֱ������AE��CD������BE��CD�ڵ�F������E��ֱ��EP��CD���ӳ��߽��ڵ�P��ʹ��PED=��C��
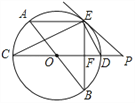
��1����֤��PE�ǡ�O�����ߣ�
��2����֤��EDƽ�֡�BEP.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
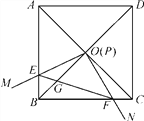
����Ŀ����ͼ���߳�Ϊ1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����ֱ�ǡ�MPN��ʹֱ�Ƕ���P���O�غϣ�ֱ�DZ�PM��PN�ֱ���OA��OB�غϣ�Ȼ����ʱ����ת��MPN����ת��Ϊ��(0�㣼�ȣ�90��)��PM��PN�ֱ�AB��BC��E��F���㣬����EF��OB�ڵ�G�������н��ۣ�(1)EF��![]() OE��(2)S�ı���OEBF��S������ABCD��1��4��(3)BE��BF��
OE��(2)S�ı���OEBF��S������ABCD��1��4��(3)BE��BF��![]() OA��(4)����ת�����У�����BEF����COF�����֮�����ʱ��AE��
OA��(4)����ת�����У�����BEF����COF�����֮�����ʱ��AE��![]() ��(5)OG��BD��AE2��CF2��������ȷ����__��
��(5)OG��BD��AE2��CF2��������ȷ����__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ε��ܳ�Ϊ![]() ���������εĵ�һ���߳�Ϊ
���������εĵ�һ���߳�Ϊ![]() ���ڶ����߳�Ϊ
���ڶ����߳�Ϊ![]() ���������߱ȵڶ����߶�
���������߱ȵڶ����߶�![]() ��
��
��1�����������ε������ߵij���
��2���������κ��������ε��ܳ��ĸ�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���![]() ��
��![]() ��
��![]() ��
��![]() .
.
(1)˵����![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
(2)��ֱ��![]() ������
������![]() ʱ����
ʱ����![]() ʱֱ��
ʱֱ��![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() �����
�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�������ABCD�У�AD��BC��E��F�DZ�BC�ϵ����㣬��BE=CF,DE��AF�ཻ������ABCD��һ��O.
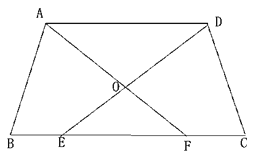
��1����֤��OE=OF;
��2����EF=ADʱ������AE��DF,���ж��ı���AEFD���������ı��Σ���֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԫ���ڼ�ij�̵���д���������ʽ���������֣�
��ʽһ��ÿ��200Ԫ��50Ԫ��
��ʽ��������۲�����400Ԫʱ����8�ۣ�����۳���400Ԫ������400Ԫ�IJ��ִ�8�ۣ�����400Ԫ�IJ��ִ�6����
��ijһ��Ʒ�ı��Ϊ![]() Ԫ��
Ԫ��
��1����![]() Ԫ������ʽ��Ӧ������Ǯ��
Ԫ������ʽ��Ӧ������Ǯ��
��2����![]() ʱ��
ʱ��![]() ȡ��ֵ���ַ�ʽ���Ż���ͬ��
ȡ��ֵ���ַ�ʽ���Ż���ͬ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com