
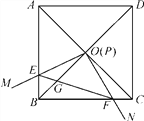
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:(1)EF=![]() OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OG·BD=AE2+CF2,其中正确的是__.
;(5)OG·BD=AE2+CF2,其中正确的是__.
【答案】(1)(2)(3)(5)
【解析】分析:
(1)由四边形ABCD是正方形,直角∠MPN,易证得△BOE≌△COF(ASA),则可证得结论;
(2)由(1)易证得S四边形OEBF=S△BOC=![]()
![]() S正方形ABCD,则可证得结论;
S正方形ABCD,则可证得结论;
(3)由BE=CF,可得BE+BF=BC,然后由等腰直角三角形的性质,证得BE+BF=![]() OA;
OA;
(4)首先设AE=x,则BE=CF=1﹣x,BF=x,继而表示出△BEF与△COF的面积之和,然后利用二次函数的最值问题,求得答案;
(5)易证得△OEG∽△OBE,然后由相似三角形的对应边成比例,证得OGOB=OE2,再利用OB与BD的关系,OE与EF的关系,即可证得结论.
【解答】解:(1)∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
 ,
,
∴△BOE≌△COF(ASA),
∴OE=OF,BE=CF,
∴EF=![]() OE;故正确;
OE;故正确;
(2)∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
∴S四边形OEBF:S正方形ABCD=1:4;故正确;
(3)∴BE+BF=BF+CF=BC=![]() OA;故正确;
OA;故正确;
(4)过点O作OH⊥BC,
∵BC=1,
∴OH=![]() BC=
BC=![]() ,
,
设AE=x,则BE=CF=1﹣x,BF=x,
∴S△BEF+S△COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]() x(1﹣x)+
x(1﹣x)+![]() (1﹣x)×
(1﹣x)×![]() =﹣
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∵a=﹣![]() <0,
<0,
∴当x=![]() 时,S△BEF+S△COF最大;
时,S△BEF+S△COF最大;
即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;故错误;
;故错误;
(5)∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OGOB=OE2,
∵OB=![]() BD,OE=
BD,OE=![]() EF,
EF,
∴OGBD=EF2,
∵在△BEF中,EF2=BE2+BF2,
∴EF2=AE2+CF2,
∴OGBD=AE2+CF2.故正确.
故答案为:(1),(2),(3),(5).




科目:初中数学 来源: 题型:
【题目】如图,数轴上有A,B两点,AB=18,原点O是线段AB上的一点,OA=2OB.
(1)求出A,B两点所表示的数;
(2)若点C是线段AO上一点,且满足 AC=CO+CB,求C点所表示的数;
(3)若点E以3个单位长度/秒的速度从点A沿数轴向点B方向匀速运动,同时点F以1个单位长度/秒的速度从点B沿数轴向右匀速运动,并设运动时间为t秒,问t为多少时,E、F两点重合.并求出此时数轴上所表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司决定更换节能环保的新型公交车![]() 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:
A型数量 | B型数量 | 所需费用 |
3 | 1 | 450 |
2 | 3 | 650 |
![]() 求A型和B型公交车的单价;
求A型和B型公交车的单价;
![]() 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为射线AB上一点,AB=30,AC比BC的![]() 多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②AB=4NQ;③当PB=
多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②AB=4NQ;③当PB=![]() BQ时,t=12,其中正确结论的个数是( )
BQ时,t=12,其中正确结论的个数是( )
![]()
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一座立交桥的示意图(道路宽度忽略不计), A为入口, F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF ;弯道为以点O为圆心的一段弧,且弧BC,弧ED,弧CD所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出. 其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法错误的是( )
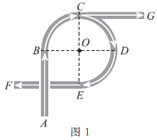

A. 甲车在立交桥上共行驶8s B. 从F口出比从G口出多行驶40m
C. 甲车从F口出,乙车从G口出 D. 立交桥总长为150m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:计算![]() (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算![]() .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() .
.

探究二:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() ,
,
两边同除以2,得![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ﹣
﹣![]() .
.

探究三:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式:_________,
所以,![]() +
+![]() +
+![]() +…+
+…+![]() =________.
=________.
拓广应用:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市米厂接到加工大米任务,要求![]() 天内加工完
天内加工完![]() 大米.米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲、乙两车间各自加工大米数量
大米.米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲、乙两车间各自加工大米数量![]() 与甲车间加工时间
与甲车间加工时间![]() (天)之间的关系如图1所示;未加工大米
(天)之间的关系如图1所示;未加工大米![]() 与甲车间加工时间
与甲车间加工时间![]() (天)之间的关系如图2所示,请结合图像回答下列问题
(天)之间的关系如图2所示,请结合图像回答下列问题

(1)甲车间每天加工大米__________;![]() =______________;
=______________;
(2)直接写出乙车间维修设备后,乙车间加工大米数量![]() 与
与![]() (天)之间的函数关系式,并指出自变量的取值范围.
(天)之间的函数关系式,并指出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:

(1)当桌子上放有![]() 个碟子时,请写出此时碟子的高度(用含
个碟子时,请写出此时碟子的高度(用含![]() 的式子表示);
的式子表示);
(2)分别从三个方向上看,其三视图如下图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
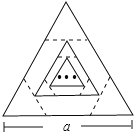
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com