
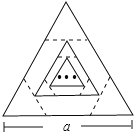
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接AD、DB、DF,求出∠AFD=∠ABD=90°,根据HL证两三角形全等得出∠FAD=60°,求出AD∥EF∥GI,过F作FZ⊥GI,过E作EN⊥GI于N,得出平行四边形FZNE得出EF=ZN=![]() a,求出GI的长,求出第一个正六边形的边长是
a,求出GI的长,求出第一个正六边形的边长是![]() a,是等边三角形QKM的边长的
a,是等边三角形QKM的边长的![]() ;同理第二个正六边形的边长是等边三角形GHI的边长的
;同理第二个正六边形的边长是等边三角形GHI的边长的![]() ;求出第五个等边三角形的边长,乘以
;求出第五个等边三角形的边长,乘以![]() 即可得出第六个正六边形的边长.
即可得出第六个正六边形的边长.
连接AD、DF、DB.
∵六边形ABCDEF是正六边形,
∴∠ABC=∠BAF=∠AFE,AB=AF,∠E=∠C=120°,EF=DE=BC=CD,
∴∠EFD=∠EDF=∠CBD=∠BDC=30°,
∵∠AFE=∠ABC=120°,
∴∠AFD=∠ABD=90°,
在Rt△ABD和RtAFD中
![]()
∴Rt△ABD≌Rt△AFD(HL),
∴∠BAD=∠FAD=![]() ×120°=60°,
×120°=60°,
∴∠FAD+∠AFE=60°+120°=180°,
∴AD∥EF,
∵G、I分别为AF、DE中点,
∴GI∥EF∥AD,
∴∠FGI=∠FAD=60°,
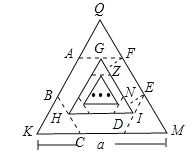
∵六边形ABCDEF是正六边形,△QKM是等边三角形,
∴∠EDM=60°=∠M,
∴ED=EM,
同理AF=QF,
即AF=QF=EF=EM,
∵等边三角形QKM的边长是a,
∴第一个正六边形ABCDEF的边长是![]() a,即等边三角形QKM的边长的
a,即等边三角形QKM的边长的![]() ,
,
过F作FZ⊥GI于Z,过E作EN⊥GI于N,
则FZ∥EN,
∵EF∥GI,
∴四边形FZNE是平行四边形,
∴EF=ZN=![]() a,
a,
∵GF=![]() AF=
AF=![]() ×
×![]() a=
a=![]() a,∠FGI=60°(已证),
a,∠FGI=60°(已证),
∴∠GFZ=30°,
∴GZ=![]() GF=
GF=![]() a,
a,
同理IN=![]() a,
a,
∴GI=![]() a+
a+![]() a+
a+![]() a=
a=![]() a,即第二个等边三角形的边长是
a,即第二个等边三角形的边长是![]() a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是![]() ×
×![]() a;
a;
同理第第三个等边三角形的边长是![]() ×
×![]() a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是![]() ×
×![]() ×
×![]() a;
a;
同理第四个等边三角形的边长是![]() ×
×![]() ×
×![]() a,第四个正六边形的边长是
a,第四个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() a;
a;
第五个等边三角形的边长是![]() ×
×![]() ×
×![]() ×
×![]() a,第五个正六边形的边长是
a,第五个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a;
a;
第六个等边三角形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a,第六个正六边形的边长是
a,第六个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a,
a,
即第六个正六边形的边长是![]() ×
×![]() a,
a,
故选A.



 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
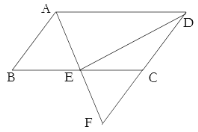
【题目】如图,平行四边形ABCD中,AD=2AB,E是BC的中点,连结AE并延长交DC的延长线于点F.
(1)求证:DE⊥AF;
(2)若∠B=60°,DE=4,求AB的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从A向点D以1cm/s的速度运动,到点D即停止.点Q从点C向点B以2cm/s的速度运动,到点B即停止.直线PQ将四边形ABCD截得两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,
, ![]() 于点
于点![]() ,且
,且![]() ,
, ![]() 是射线
是射线![]() 上一动点,
上一动点, ![]() 、
、![]() 分别是
分别是![]() ,
, ![]() 的中点,过点
的中点,过点![]() ,
, ![]() ,
, ![]() 的圆与
的圆与![]() 的另一交点
的另一交点![]() (点
(点![]() 在线段
在线段![]() 上),连结
上),连结![]() ,
, ![]() .
.

(![]() )当
)当![]() 时,则
时,则![]() 的度数为__________.
的度数为__________.
(![]() )在点
)在点![]() 的运动过程中,当
的运动过程中,当![]() 时,取四边形
时,取四边形![]() 一边的两端点和线段
一边的两端点和线段![]() 上一点
上一点![]() ,若以这三点为顶点的三角形是直角三角形,当
,若以这三点为顶点的三角形是直角三角形,当![]() 时,则
时,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个运输公司有甲、乙两种货车,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运货吨数 | |
第一次 | 2 | 4 | 18 |
第二次 | 5 | 6 | 35 |
(1)求甲、乙两种货车每次满载分别能运输多少吨货物;
(2)现有一批重34吨的货物需要运输,而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输,为了使保养费用不超过700元,公司该如何安排甲、乙两种货车来完成这次运输任务.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,分别交BC于点D、E,已知△ADE的周长5cm.
(1)求BC的长;
(2)分别连接OA、OB、OC,若△OBC的周长为13cm,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是( )
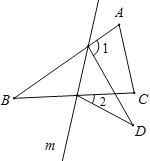
A. 32° B. 64° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线 AB 分别交 x 轴、y 轴于点A(–a,0)、点 B(0, b),且 a、b 满足a2+b2–4a–8b+20=0,点 P 在直线 AB 的右侧,且∠APB=45°.

(1)a= ;b= .
(2)若点 P 在 x 轴上,请在图中画出图形(BP 为虚线),并写出点 P 的坐标;
(3)若点 P 不在 x 轴上,是否存在点P,使△ABP 为直角三角形?若存在,请求出此时P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
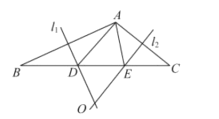
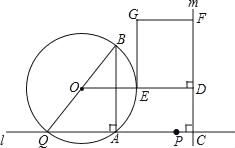
【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com