[题目]甲三角形的周长为.乙三角形的第一条边长为.第二条边长为.第三条边比第二条边短．(1)求乙三角形第三条边的长,(2)甲三角形和乙三角形的周长哪个大?试说明理由．题目和参考答案——青夏教育精英家教网—

【题目】甲三角形的周长为，乙三角形的第一条边长为，第二条边长为，第三条边比第二条边短．

（1）求乙三角形第三条边的长；

（2）甲三角形和乙三角形的周长哪个大？试说明理由．

【答案】（1）-b+5；（2）甲三角形的周长较大，理由见解析

【解析】

（1）根据第二条边长为a2-3b，第三条边比第二条边短a2-2b-5．可求出第三条边；
（2）求出乙三角形的周长，再利用作差法，和非负数的意义做出判断即可.

解：（1）由题意得，（a2-3b）-（a2-2b-5）=-b+5，
∴乙三角形第三条边的长为-b+5，
（2）乙三角形的周长为：（a2-2b）+（a2-3b）+（-b+5）=2a2-6b+5，
甲、乙三角形的周长的差为：（3a2-6b+8）-（2a2-6b+5）=a2+3＞0，
∴甲三角形的周长较大.

练习册系列答案

暑假作业与生活陕西师范大学出版总社有限公司系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图1，四边形ABCD是菱形，AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M，连接BM，且AH=3．

（1）求证:DM=BM；

（2）求MH的长；

（3）如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式；

（4）在（3）的条件下，当点P在边AB上运动时是否存在这样的 t值，使∠MPB与∠BCD互为余角，若存在,则求出t值，若不存，在请说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：二次函数的图象与x轴交于点A、，顶点为

求该二次函数的解析式；

如图，过A、C两点作直线，并将线段AC沿该直线向上平移，记点A、C分别平移到点D、E处若点F在这个二次函数的图象上，且是以EF为斜边的等腰直角三角形，求点F的坐标；

试确定实数p，q的值，使得当时，．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，图1中小正方形的个数为1个；图2中小正方形的个数为：1+3＝4＝22个；图3中小正方形的个数为：1+3+5＝9＝32个；图4中小正方形的个数为：1+3+5+7＝16＝42个；…

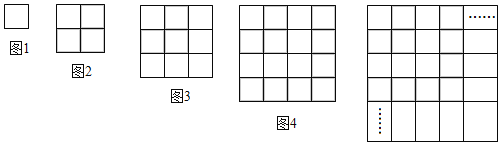
（1）根据你的发现，第n个图形中有小正方形：1+3+5+7+…+　　＝　　个．

（2）由（1）的结论，解答下列问题：已知连续奇数的和：（2n+1）+（2n+3）+（2n+5）+……+137+139＝3300，求n的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】数学问题：计算（其中m，n都是正整数，且m≥2，n≥1）．

探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．

探究一：计算．

第1次分割，把正方形的面积二等分，其中阴影部分的面积为；

第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为+；

第3次分割，把上次分割图中空白部分的面积继续二等分，…；

…

第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为+++…+，最后空白部分的面积是．

根据第n次分割图可得等式： +++…+=1﹣．

探究二：计算+++…+．

第1次分割，把正方形的面积三等分，其中阴影部分的面积为；

第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为+；

第3次分割，把上次分割图中空白部分的面积继续三等分，…；

…

第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为+++…+，最后空白部分的面积是．

根据第n次分割图可得等式： +++…+=1﹣，

两边同除以2，得+++…+=﹣．

探究三：计算+++…+．

（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）

解决问题：计算+++…+．

（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）

根据第n次分割图可得等式：_________，

所以， +++…+=________．

拓广应用：计算 +++…+．

查看答案和解析>>

科目：初中数学 来源： 题型：

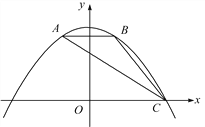
【题目】如图，抛物线y＝ax2＋bx＋c经过△ABC的三个顶点，与y轴相交于(0， )，点A坐标为(－1，2)，点B是点A关于y轴的对称点，点C在x轴的正半轴上．

（1）求该抛物线的函数解析式；

（2）点F为线段AC上一动点，过点F作FE⊥x轴，FG⊥y轴，垂足分别为点E，G，当四边形OEFG为正方形时，求出点F的坐标；

（3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，正方形ABCD中，BD为对角线．

（1）尺规作图：作CD边的垂直平分线EF，交CD于点E，交BD于点F（保留作图痕迹，不要求写作法）；

（2）在（1）的条件下，若AB=4，求△DEF的周长．

查看答案和解析>>

科目：初中数学 来源： 题型：

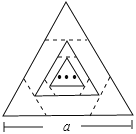
【题目】边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）