
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2ЃЋbxЃЋcОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌгыyжсЯрНЛгк(0ЃЌ ![]() )ЃЌЕуAзјБъЮЊ(Ѓ1ЃЌ2)ЃЌЕуBЪЧЕуAЙигкyжсЕФЖдГЦЕуЃЌЕуCдкxжсЕФе§АыжсЩЯЃЎ
)ЃЌЕуAзјБъЮЊ(Ѓ1ЃЌ2)ЃЌЕуBЪЧЕуAЙигкyжсЕФЖдГЦЕуЃЌЕуCдкxжсЕФе§АыжсЩЯЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
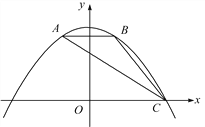
ЃЈ2ЃЉЕуFЮЊЯпЖЮACЩЯвЛЖЏЕуЃЌЙ§ЕуFзїFEЁЭxжсЃЌFGЁЭyжсЃЌДЙзуЗжБ№ЮЊЕуEЃЌGЃЌЕБЫФБпаЮOEFGЮЊе§ЗНаЮЪБЃЌЧѓГіЕуFЕФзјБъЃЛ
ЃЈ3ЃЉНЋЃЈ2ЃЉжаЕФе§ЗНаЮOEFGбиOCЯђгвЦНвЦЃЌМЧЦНвЦжаЕФе§ЗНаЮOEFGЮЊе§ЗНаЮDEFGЃЌЕБЕуEКЭЕуCжиКЯЪБЭЃжЙдЫЖЏЃЌЩшЦНвЦЕФОрРыЮЊtЃЌе§ЗНаЮЕФБпEFгыACНЛгкЕуMЃЌDGЫљдкЕФжБЯпгыACНЛгкЕуNЃЌСЌНгDMЃЌЪЧЗёДцдкетбљЕФtЃЌЪЙЁїDMNЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љ![]() x2+
x2+![]() ЃЛЃЈ2ЃЉЃЈ1ЃЌ1ЃЉЃЛЃЈ3ЃЉЕБЁїDMNЪЧЕШбќШ§НЧаЮЪБЃЌtЕФжЕЮЊ
ЃЛЃЈ2ЃЉЃЈ1ЃЌ1ЃЉЃЛЃЈ3ЃЉЕБЁїDMNЪЧЕШбќШ§НЧаЮЪБЃЌtЕФжЕЮЊ![]() ЃЌ3Љ
ЃЌ3Љ![]() Лђ1ЃЎ
Лђ1ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉвзЕУХзЮяЯпЕФЖЅЕуЮЊЃЈ0ЃЌ![]() ЃЉЃЌШЛКѓжЛашдЫгУД§ЖЈЯЕЪ§ЗЈЃЌОЭПЩЧѓГіХзЮяЯпЕФКЏЪ§ЙиЯЕБэДяЪНЃЛ
ЃЉЃЌШЛКѓжЛашдЫгУД§ЖЈЯЕЪ§ЗЈЃЌОЭПЩЧѓГіХзЮяЯпЕФКЏЪ§ЙиЯЕБэДяЪНЃЛ
ЃЈ2ЃЉЂйЕБЕуFдкЕквЛЯѓЯоЪБЃЌШчЭМ1ЃЌПЩЧѓГіЕуCЕФзјБъЃЌжБЯпACЕФНтЮіЪНЃЌЩше§ЗНаЮOEFGЕФБпГЄЮЊpЃЌдђFЃЈpЃЌpЃЉЃЌДњШыжБЯпACЕФНтЮіЪНЃЌОЭПЩЧѓГіЕуFЕФзјБъЃЛЂкЕБЕуFдкЕкЖўЯѓЯоЪБЃЌЭЌРэПЩЧѓГіЕуFЕФзјБъЃЌДЫЪБЕуFВЛдкЯпЖЮACЩЯЃЌЙЪЩсШЅЃЛ
ЃЈ3ЃЉЙ§ЕуMзїMHЁЭDNгкHЃЌШчЭМ2ЃЌгЩЬтПЩЕУ0ЁмtЁм2ЃЎШЛКѓжЛашгУtЕФЪНзгБэЪОDNЁЂDM2ЁЂMN2ЃЌЗжШ§жжЧщПіЃЈЂйDN=DMЃЌЂкND=NMЃЌЂлMN=MDЃЉЬжТлОЭПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпЕуBЪЧЕуAЙигкyжсЕФЖдГЦЕуЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЮЊyжсЃЌ
ЁрХзЮяЯпЕФЖЅЕуЮЊЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЙЪХзЮяЯпЕФНтЮіЪНПЩЩшЮЊy=ax2+![]() ЃЎ
ЃЎ
ЁпAЃЈЉ1ЃЌ2ЃЉдкХзЮяЯпy=ax2+![]() ЩЯЃЌ
ЩЯЃЌ
Ёрa+![]() =2ЃЌ
=2ЃЌ
НтЕУa=Љ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФКЏЪ§ЙиЯЕБэДяЪНЮЊy=Љ![]() x2+
x2+![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЕБЕуFдкЕквЛЯѓЯоЪБЃЌШчЭМ1ЃЌ
Сюy=0ЕУЃЌЉ![]() x2+
x2+![]() =0ЃЌ
=0ЃЌ
НтЕУЃКx1=3ЃЌx2=Љ3ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЎ
ЩшжБЯпACЕФНтЮіЪНЮЊy=mx+nЃЌ
дђга![]() ЃЌ
ЃЌ
НтЕУ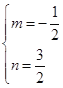 ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊy=Љ![]() x+
x+![]() ЃЎ
ЃЎ
Щше§ЗНаЮOEFGЕФБпГЄЮЊpЃЌдђFЃЈpЃЌpЃЉЃЎ
ЁпЕуFЃЈpЃЌpЃЉдкжБЯпy=Љ![]() x+
x+![]() ЩЯЃЌ
ЩЯЃЌ
ЁрЉ![]() p+
p+![]() =pЃЌ
=pЃЌ
НтЕУp=1ЃЌ
ЁрЕуFЕФзјБъЮЊЃЈ1ЃЌ1ЃЉЃЎ
ЂкЕБЕуFдкЕкЖўЯѓЯоЪБЃЌ
ЭЌРэПЩЕУЃКЕуFЕФзјБъЮЊЃЈЉ3ЃЌ3ЃЉЃЌ
ДЫЪБЕуFВЛдкЯпЖЮACЩЯЃЌЙЪЩсШЅЃЎ
злЩЯЫљЪіЃКЕуFЕФзјБъЮЊЃЈ1ЃЌ1ЃЉЃЛ
ЃЈ3ЃЉЙ§ЕуMзїMHЁЭDNгкHЃЌШчЭМ2ЃЌ
дђOD=tЃЌOE=t+1ЃЎ
ЁпЕуEКЭЕуCжиКЯЪБЭЃжЙдЫЖЏЃЌЁр0ЁмtЁм2ЃЎ
ЕБx=tЪБЃЌy=Љ![]() t+
t+![]() ЃЌдђNЃЈtЃЌЉ
ЃЌдђNЃЈtЃЌЉ![]() t+
t+![]() ЃЉЃЌDN=Љ
ЃЉЃЌDN=Љ![]() t+
t+![]() ЃЎ
ЃЎ
ЕБx=t+1ЪБЃЌy=Љ![]() ЃЈt+1ЃЉ+
ЃЈt+1ЃЉ+![]() =Љ
=Љ![]() t+1ЃЌдђMЃЈt+1ЃЌЉ
t+1ЃЌдђMЃЈt+1ЃЌЉ![]() t+1ЃЉЃЌME=Љ
t+1ЃЉЃЌME=Љ![]() t+1ЃЎ
t+1ЃЎ
дкRtЁїDEMжаЃЌDM2=12+ЃЈЉ![]() t+1ЃЉ2=
t+1ЃЉ2=![]() t2Љt+2ЃЎ
t2Љt+2ЃЎ
дкRtЁїNHMжаЃЌMH=1ЃЌNH=ЃЈЉ![]() t+
t+![]() ЃЉЉЃЈЉ
ЃЉЉЃЈЉ![]() t+1ЃЉ=
t+1ЃЉ=![]() ЃЌ
ЃЌ
ЁрMN2=12+ЃЈ![]() ЃЉ2=
ЃЉ2=![]() ЃЎ
ЃЎ
ЂйЕБDN=DMЪБЃЌ
ЃЈЉ![]() t+
t+![]() ЃЉ2=
ЃЉ2=![]() t2Љt+2ЃЌ
t2Љt+2ЃЌ
НтЕУt=![]() ЃЛ
ЃЛ
ЂкЕБND=NMЪБЃЌ
Љ![]() t+
t+![]() =
=![]() ЃЌ
ЃЌ
НтЕУt=3Љ![]() ЃЛ
ЃЛ
ЂлЕБMN=MDЪБЃЌ
![]() =
=![]() t2Љt+2ЃЌ
t2Љt+2ЃЌ
НтЕУt1=1ЃЌt2=3ЃЎ
Ёп0ЁмtЁм2ЃЌЁрt=1ЃЎ
злЩЯЫљЪіЃКЕБЁїDMNЪЧЕШбќШ§НЧаЮЪБЃЌtЕФжЕЮЊ![]() ЃЌ3Љ
ЃЌ3Љ![]() Лђ1ЃЎ
Лђ1ЃЎ


 МЦЫуИпЪжЯЕСаД№АИ
МЦЫуИпЪжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЙФРјЪаУёНкдМгУЫЎЃЌФГЪаОгУёЩњЛюгУЫЎАДНзЬнЪНЫЎМлМЦЗб.ЯТБэЪЧИУЪаУёвЛЛЇвЛБэ"ЩњЛюгУЫЎНзЬнЪНМЦЗбМлИёБэЕФВПЗжаХЯЂ:
здРДЫЎЯњЪлМлИё | ЮлЫЎДІРэМлИё | |
УПЛЇУПдТгУЫЎСП | ЕЅМл:дЊ/Жж | ЕЅМл:дЊ/Жж |
|
|
|
ГЌЙ§ |
|
|
ГЌЙ§ |
|
|
(ЫЕУї:УПЛЇЩњВњЕФЮлЫЎСПЕШгкИУЛЇздРДЫЎгУСП;ЂкЫЎЗб=здРДЫЎЗбгУ+ЮлЫЎДІРэЗб)
вбжЊаЁЭѕМв2018Фъ7дТгУЫЎ![]() ЖжЃЌНЛЫЎЗб
ЖжЃЌНЛЫЎЗб![]() дЊ.8дТЗнгУЫЎ
дЊ.8дТЗнгУЫЎ![]() ЖжЃЌНЛЫЎЗб
ЖжЃЌНЛЫЎЗб![]() дЊ.
дЊ.
ЃЈ1ЃЉЧѓ![]() ЕФжЕ;
ЕФжЕ;
ЃЈ2ЃЉШчЙћаЁЭѕМв9дТЗнЩЯНЛЫЎЗб![]() дЊЃЌдђаЁЭѕМветИідТгУЫЎЖрЩйЖж?
дЊЃЌдђаЁЭѕМветИідТгУЫЎЖрЩйЖж?
ЃЈ3ЃЉаЁЭѕМв10дТЗнЭќМЧСЫШЅНЛЫЎЗбЃЌЕБЫћ11дТШЅНЛЫЎЗбЪБЗЂЯжСНИідТвЛЙВгУЫЎ50ЖжЃЌЦфжа10дТЗнгУЫЎГЌЙ§![]() ЖжЃЌвЛЙВНЛЫЎЗб
ЖжЃЌвЛЙВНЛЫЎЗб![]() дЊЃЌЦфжаАќКЌ
дЊЃЌЦфжаАќКЌ![]() дЊжЭФЩН№ЃЌЧѓаЁЭѕМв11дТЗнгУЫЎЖрЩйЖж? (жЭФЩН№:вђЮДФмАДЦкНЩФЩЫЎЗбЃЌгтЦквЊНЩФЩЕФЁАЗЃПюН№ЖюЁБ)
дЊжЭФЩН№ЃЌЧѓаЁЭѕМв11дТЗнгУЫЎЖрЩйЖж? (жЭФЩН№:вђЮДФмАДЦкНЩФЩЫЎЗбЃЌгтЦквЊНЩФЩЕФЁАЗЃПюН№ЖюЁБ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжгаЮхеХаЮзДЁЂДѓаЁЁЂжЪЕиЖМЯрЭЌЕФПЈЦЌЃЌетаЉПЈЦЌЩЯУцЗжБ№ЛгаЯТСаЭМаЮЃКЂйе§ЗНаЮЃЛЂкЕШБпШ§НЧаЮЃЛЂлЦНааЫФБпаЮЃЛЂмЕШбќШ§НЧаЮЃЛЂндВЃЎНЋПЈЦЌБГУцГЏЩЯЯДдШЃЌДгжаЫцЛњГщШЁвЛеХЃЌГщГіЕФжНЦЌе§УцЭМаЮЪЧжсЖдГЦЭМаЮЃЌЕЋВЛЪЧжааФЖдГЦЭМаЮЕФИХТЪЪЧЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪщЕъЮЊСЫгНгЁАЖСЪщНкЁБжЦЖЈСЫЛюЖЏМЦЛЎЃЌвдЯТЪЧЛюЖЏМЦЛЎЪщЕФВПЗжаХЯЂЃК
ЁАЖСЪщНкЁБЛюЖЏМЦЛЎЪщ | ||
ЪщБОРрБ№ | AРр | BРр |
НјМл(ЕЅЮЛЃКдЊ) | 18 | 12 |
БИзЂ | 1.гУВЛГЌЙ§16800дЊЙКНјAЃЌBСНРрЭМЪщЙВ1000БОЃЛ 2ЃЎAРрЭМЪщВЛЩйгк600БОЃЛ ЁЁ |
(1)ГТОРэВщПДМЦЛЎЪ§ЪБЗЂЯжЃКAРрЭМЪщЕФБъМлЪЧBРрЭМЪщБъМлЕФ1.5БЖЃЌШєЙЫПЭгУ540дЊЙКТђЭМЪщЃЌФмЕЅЖРЙКТђAРрЭМЪщЕФЪ§СПЧЁКУБШЕЅЖРЙКТђBРрЭМЪщЕФЪ§СПЩй10БОЃЌЧыЧѓГіAЃЌBСНРрЭМЪщЕФБъМлЃЛ
(2)ОЪаГЁЕїВщКѓЃЌГТОРэЗЂЯжЫћУЧИпЙРСЫЁАЖСЪщНкЁБЖдЭМЪщЯњЪлЕФгАЯьЃЌБуЕїећСЫЯњЪлЗНАИЃЌAРрЭМЪщУПБОБъМлНЕЕЭaдЊ(0ЃМaЃМ5)ЯњЪлЃЌBРрЭМЪщМлИёВЛБфЃЌФЧУДЪщЕъгІШчКЮНјЛѕВХФмЛёЕУзюДѓРћШѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзШ§НЧаЮЕФжмГЄЮЊ![]() ЃЌввШ§НЧаЮЕФЕквЛЬѕБпГЄЮЊ
ЃЌввШ§НЧаЮЕФЕквЛЬѕБпГЄЮЊ![]() ЃЌЕкЖўЬѕБпГЄЮЊ
ЃЌЕкЖўЬѕБпГЄЮЊ![]() ЃЌЕкШ§ЬѕБпБШЕкЖўЬѕБпЖЬ
ЃЌЕкШ§ЬѕБпБШЕкЖўЬѕБпЖЬ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓввШ§НЧаЮЕкШ§ЬѕБпЕФГЄЃЛ
ЃЈ2ЃЉМзШ§НЧаЮКЭввШ§НЧаЮЕФжмГЄФФИіДѓЃПЪдЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЪЧЁїABCЕФНЧЦНЗжЯпЃЌНЋЁїABCелЕўЪЙЕуAТфдкЕуDДІЃЌелКлЮЊEFЃЌдђЫФБпаЮAEDFвЛЖЈЪЧЃЈЁЁЁЁЃЉ

A. ОиаЮ B. СтаЮ C. е§ЗНаЮ D. ЬнаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЪЎЁЄвЛЁБЛЦН№жмЦкМф,еХМвНчЗчОАЧјдк7ЬьМйЦкжаУПЬьТУгЮШЫЪ§БфЛЏШчЯТБэ(е§КХБэЪОШЫЪ§БШЧАвЛЬьЖр,ИККХБэЪОБШЧАЬьЩй)
ШеЦк | 1Ше | 2Ше | 3Ше | 4Ше | 5Ше | 6Ше | 7Ше |
ШЫЪ§БфЛЏ ЕЅЮЛЃКЭђШЫ | +1.8 | -0.6 | +0.2 | -0.7 | -1.3 | +0.5 | -2.4 |
(1)Шє9дТ30ШеЕФТУПЭШЫЪ§ЮЊ![]() ЭђШЫЃЌдђ10дТ4ШеЕФТУПЭШЫЪ§ЮЊ_______ЭђШЫ;
ЭђШЫЃЌдђ10дТ4ШеЕФТУПЭШЫЪ§ЮЊ_______ЭђШЫ;
(2)ЦпЬьжаТУПЭШЫЪ§зюЖрЕФвЛЬьБШзюЩйЕФвЛЬьЖр______ЭђШЫ;
(3)ШчЙћУПЭђШЫДјРДЕФОМУЪеШыдМЮЊ120ЭђдЊ,дђЛЦН№жмЦпЬьЕФТУгЮзмЪеШыдМЮЊЖрЩйЭђдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїDAC КЭЁїEBC ОљЪЧЕШБпШ§НЧаЮЃЌAЃЌCЃЌB Ш§ЕудквЛЬѕжБЯпЩЯЃЌAEЃЌBD ЗжБ№гы CDЁЂCE НЛгкЕу MЁЂNЃЌAEЃЌBD ЯрНЛгкЕу O.
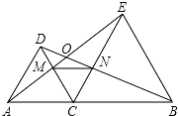
ЃЈ1ЃЉЧѓжЄЃКЁїACE ЁеЁїDCB;
ЃЈ2ЃЉЧѓЁЯAOD ЕФЖШЪ§
ЃЈ3ЃЉХаЖЯЁїCMN ЕФаЮзДВЂЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=Љx2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌOB=OC=3ЃЌжБЯпlЪЧХзЮяЯпЕФЖдГЦжсЃЌEЪЧХзЮяЯпЕФЖЅЕуЃЎ
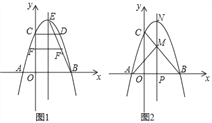
ЃЈIЃЉЧѓbЃЌcЕФжЕЃЛ
ЃЈЂђЃЉШчЭМ1ЃЌСЌBEЃЌЯпЖЮOCЩЯЕФЕуFЙигкжБЯпlЕФЖдГЦЕуFЁфЧЁКУдкЯпЖЮBEЩЯЃЌЧѓЕуFЕФзјБъЃЛ
ЃЈЂѓЃЉШчЭМ2ЃЌЖЏЕуPдкЯпЖЮOBЩЯЃЌЙ§ЕуPзїxжсЕФДЙЯпЗжБ№гыBCНЛгкЕуMЁЂгыХзЮяЯпНЛгкЕуNЃЎЪдЮЪЃКХзЮяЯпЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУЁїPQNгыЁїAPMЕФУцЛ§ЯрЕШЃЌЧвЯпЖЮNQЕФГЄЖШзюаЁЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com