
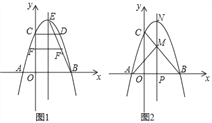
【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC=3,直线l是抛物线的对称轴,E是抛物线的顶点.
(I)求b,c的值;
(Ⅱ)如图1,连BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(Ⅲ)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
【答案】(I)b=2,c=3;;(Ⅱ)F的坐标为(0,2);(Ⅲ)见解析.
【解析】分析:(I)将点B、C的坐标代入函数解析式求得系数b、c的值即可;
(Ⅱ)可设F(0,m),则可表示出F′的坐标,由B、E的坐标可求得直线BE的解析式,把F′坐标代入直线BE解析式可得到关于m的方程,可求得F点的坐标;
(Ⅲ)设点P坐标为(n,0),可表示出PA、PB、PN的长,作QR⊥PN,垂足为R,则可求得QR的长,用n可表示出Q、R、N的坐标,在Rt△QRN中,由勾股定理可得到关于n的二次函数,利用二次函数的性质可知其取得最小值时n的值,则可求得Q点的坐标.
详解:(I)∵OB=OC=3,
∴B(3,0),C(0,3),
将其代入y=-x2+bx+c,得
![]() ,
,
解得b=2,c=3;
(Ⅱ)设点F的坐标为(0,m).
∵对称轴为直线x=1,
∴点F关于直线l的对称点F的坐标为(2,m).
由(I)可知抛物线解析式为y=-x2+2x+3=-(x-1)2+4,
∴E(1,4),
∵直线BE经过点B(3,0),E(1,4),
∴利用待定系数法可得直线BE的表达式为y=-2x+6.
∵点F在BE上,
∴m=-2×2+6=2,即点F的坐标为(0,2);
(Ⅲ)存在点Q满足题意.
设点P坐标为(n,0),则PA=n+1,PB=PM=3-n,PN=-n2+2n+3.
作QR⊥PN,垂足为R,

∵S△PQN=S△APM,
∴![]() (n+1)(3-n)=
(n+1)(3-n)=![]() (-n2+2n+3)QR,
(-n2+2n+3)QR,
∴QR=1.
①点Q在直线PN的左侧时,Q点的坐标为(n-1,-n2+4n),R点的坐标为(n,-n2+4n),N点的坐标为(n,-n2+2n+3).
∴在Rt△QRN中,NQ2=1+(2n-3)2,
∴n=![]() 时,NQ取最小值1.此时Q点的坐标为(
时,NQ取最小值1.此时Q点的坐标为(![]() ,
,![]() );
);
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2-4).
同理,NQ2=1+(2n-1)2,
∴n=![]() 时,NQ取最小值1.此时Q点的坐标为(
时,NQ取最小值1.此时Q点的坐标为(![]() ,
,![]() ).
).
综上可知存在满足题意的点Q,其坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
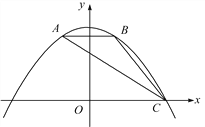
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
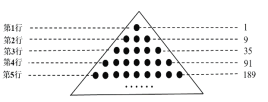
【题目】如图,一个点表示一个数,不同位置的点表示不同的数,每行各点所表示的数自左向右从小到大,且相邻两个点所表示的数相差1,每行数的和等于右边相应的数字,那么,表示2020的点在第______行,从左向右第______个位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】12月4日为全国法制宣传日,当天某初中组织4名学生参加法制知识竞赛,共设20道选择题,各题分值相同,每题必答,下表记录了其中2名参赛学生的得分情况.
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 17 | 3 | 79 |
(1)参赛学生![]() 得72分,他答对了几道题?答错了几道题?
得72分,他答对了几道题?答错了几道题?
(2)参赛学生![]() 说他可以得88分,你认为可能吗?为什么?
说他可以得88分,你认为可能吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年“双十一”购物活动,商家都会利用这个契机进行打折满减的促销活动.某商家平时的优惠措施是按所有商品标价打七折:“双十一”活动期间的优惠措施是:购买的所有商品先按标价总和打七五折,再享受折后每满![]() 元减
元减![]() 元的优惠.如标价为
元的优惠.如标价为![]() 元的商品,折后为
元的商品,折后为![]() 元,再减
元,再减![]() 元,即实付:
元,即实付:![]() (元).
(元).
(1)该商店标价总和为![]() 元的商品,在“双十一”购买,最后实际支付只需多少元?
元的商品,在“双十一”购买,最后实际支付只需多少元?
(2)小明妈妈在这次活动中打算购买某件商品,打折满减后,应付金额是![]() 元,求该商品的标价.
元,求该商品的标价.
(3)在(2)的条件下,若该商家出售的商品标价均为整数,小明通过计算后告诉妈妈:通过凑单(再购买少量商品)实际支付金额只需再多付 元,就可获得最大优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列式子,按一定规律排列成![]() , ….
, ….
(1)当a =1时,其中三个相邻数的和是63,则位于这三个数中间的数是________;
(2)上列式子中第n个式子为_____________(n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距180km,一列慢车以40km/h的速度从甲地匀速驶往乙地,慢车出发30分钟后,一列快车以60km/h的速度从甲地匀速驶往乙地.两车相继到达终点乙地,再次过程中,两车恰好相距10km的次数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com