
【题目】有一列式子,按一定规律排列成![]() , ….
, ….
(1)当a =1时,其中三个相邻数的和是63,则位于这三个数中间的数是________;
(2)上列式子中第n个式子为_____________(n为正整数).
【答案】-27 (-3)nan2+1.
【解析】
(1)将a=1代入已知数列,可以发现该数列的通式为:(-3)n.然后根据限制性条件“三个相邻数的和是63”列出方程(-3)n-1+(-3)n+(-3)n+1=63.通过解方程即可求得(-3)n的值;
(2)利用归纳法来求已知数列的通式.
解:(1)当a=1时,则
-3=(-3)1,
9=(-3)2,
-27=(-3)3,
81=(-3)4,
-243=(-3)5,
则(-3)n-1+(-3)n+(-3)n+1=63,即-![]() (-3)n+(-3)n-3(-3)n=63,
(-3)n+(-3)n-3(-3)n=63,
所以-![]() (-3)n=63,
(-3)n=63,
解得,(-3)n=-27.
(2)∵第一个式子:-3a2=(-3)1a12+1,
第二个式子:9a5=(-3)2a22+1,
第三个式子:-27a10=(-3)3a32+1,
第四个式子:81a17=(-3)4a42+1,
….
则第n个式子为:(-3)nan2+1(n为正整数).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】“十·一”黄金周期间,张家界风景区在7天假期中每天旅游人数变化如下表(正号表示人数比前一天多,负号表示比前天少)
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.8 | -0.6 | +0.2 | -0.7 | -1.3 | +0.5 | -2.4 |
(1)若9月30日的旅客人数为![]() 万人,则10月4日的旅客人数为_______万人;
万人,则10月4日的旅客人数为_______万人;
(2)七天中旅客人数最多的一天比最少的一天多______万人;
(3)如果每万人带来的经济收入约为120万元,则黄金周七天的旅游总收入约为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
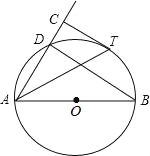
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过![]() 上一点T作⊙O的切线TC,且TC⊥AD于点C.
上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,CT=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,OB=OC=3,直线l是抛物线的对称轴,E是抛物线的顶点.
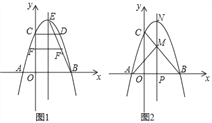
(I)求b,c的值;
(Ⅱ)如图1,连BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(Ⅲ)如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sin α·sin β的值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
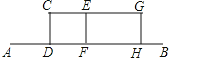
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=![]() (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
(1)求点D的坐标;
(2)点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,网格图由边长为1的小正方形所构成,Rt△ABC的顶点分别是A(-1,3),B(-3,-1),C(-3,3).

(1)请在图1中作出△ABC关于点(-1,0)成中心对称△![]() ,并分别写出A,C对应点的坐标
,并分别写出A,C对应点的坐标![]() ;
;![]()
(2)设线段AB所在直线的函数表达式为![]() ,试写出不等式
,试写出不等式![]() 的解集是 ;
的解集是 ;
(3)点M和点N 分别是直线AB和y轴上的动点,若以![]() ,
,![]() ,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
,M,N为顶点的四边形是平行四边形,求满足条件的M点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
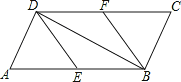
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com