
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过![]() 上一点T作⊙O的切线TC,且TC⊥AD于点C.
上一点T作⊙O的切线TC,且TC⊥AD于点C.
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,CT=![]() ,求AD的长.
,求AD的长.
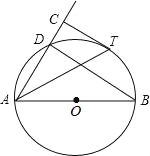
【答案】(1)、65°;(2)、2.
【解析】
试题分析:(1)、连接OT,根据同角的余角相等得出∠CAD=∠ATO,进而得出∠DAB=2CAT,解答即可;(2)、过O作OE⊥AC于E,连接OT、OD,得出矩形OECT,求出OT=CE,根据垂径定理求出DE,根据矩形性质求出OT=CT,根据勾股定理求出即可.
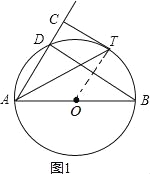
试题解析:(1)、连接OT,如图1:
∵TC⊥AD,⊙O的切线TC, ∴∠ACT=∠OTC=90°, ∴∠CAT+∠CTA=∠CTA+∠ATO, ∴∠CAT=∠ATO,
∵OA=OT, ∴∠OAT=∠ATO, ∴∠DAB=2∠CAT=50°, ∴∠CAT=25°, ∴∠ATC=90°﹣25°=65°;
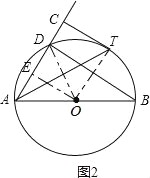
(2)、过O作OE⊥AC于E,连接OT、OD,如图2:
∵AC⊥CT,CT切⊙O于T, ∴∠OEC=∠ECT=∠OTC=90°, ∴四边形OECT是矩形,
∴OT=CE=OD=2, ∵OE⊥AC,OE过圆心O, ∴AE=DE=![]() AD, ∵CT=OE=
AD, ∵CT=OE=![]() ,
,
在Rt△OED中,由勾股定理得:ED=1, ∴AD=2.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
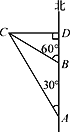
【题目】如图,一艘轮船以每小时40海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上.当轮船到达灯塔C的正东方向D处时,又航行了多少海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂第一车间有x人,第二车间比第一车间人数的 ![]() 少30人,如果从第二车间调出10人到第一车间,那么:
少30人,如果从第二车间调出10人到第一车间,那么:
(1)两个车间共有多少人?
(2)调动后,第一车间的人数比第二车间多多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com