
【题目】如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sin α·sin β的值为____.

【答案】![]()
【解析】分析:首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,由A、B两点的坐标分别为(-1,y1)、(3,y2),S△AOC=1,可求得OD,OE,OC的长,继而求得△AOB的面积,求得OAOB的值,又由三角函数的定义,即可求得答案.
详解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,
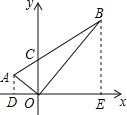
∵A、B两点的坐标分别为(-1,y1)、(3,y2),
∴OD=1,OE=3,
∵S△AOC=1,
∴![]() OCOD=1,
OCOD=1,
∴OC=2,
∴SRt△AOB=S△AOC+S△BOC=1+![]() OCOE=1+3=4,
OCOE=1+3=4,
∴![]() OAOB=4,
OAOB=4,
∴OAOB=8,
∵OA∥OC∥BE,
∴∠OAD=∠AOC=α,∠OBE=∠BOC=β,
∴sinαsinβ=![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,BD为对角线.
(1)尺规作图:作CD边的垂直平分线EF,交CD于点E,交BD于点F(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若AB=4,求△DEF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年“双十一”购物活动,商家都会利用这个契机进行打折满减的促销活动.某商家平时的优惠措施是按所有商品标价打七折:“双十一”活动期间的优惠措施是:购买的所有商品先按标价总和打七五折,再享受折后每满![]() 元减
元减![]() 元的优惠.如标价为
元的优惠.如标价为![]() 元的商品,折后为
元的商品,折后为![]() 元,再减
元,再减![]() 元,即实付:
元,即实付:![]() (元).
(元).
(1)该商店标价总和为![]() 元的商品,在“双十一”购买,最后实际支付只需多少元?
元的商品,在“双十一”购买,最后实际支付只需多少元?
(2)小明妈妈在这次活动中打算购买某件商品,打折满减后,应付金额是![]() 元,求该商品的标价.
元,求该商品的标价.
(3)在(2)的条件下,若该商家出售的商品标价均为整数,小明通过计算后告诉妈妈:通过凑单(再购买少量商品)实际支付金额只需再多付 元,就可获得最大优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列式子,按一定规律排列成![]() , ….
, ….
(1)当a =1时,其中三个相邻数的和是63,则位于这三个数中间的数是________;
(2)上列式子中第n个式子为_____________(n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,把表示数1的点称为基准点,记作点![]() .对于两个不同的点M和N,若点M、点N到点
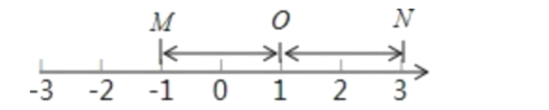
.对于两个不同的点M和N,若点M、点N到点![]() 的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点
的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点![]() 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b=_________;若a=4,则b=_________;
②用含a的式子表示b,则b=____________;
(2)对点A进行如下操作:先把点A表示的数乘以2.5,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是___________;
(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,…,依此顺序不断地重复,得到
的基准变换点,…,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .
.![]() 为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
,![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,…,依此顺序不断地重复,得到
,…,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .若无论k为何值,
.若无论k为何值,![]() 与
与![]() 两点间的距离都是4,则n=__________
两点间的距离都是4,则n=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个工程队承包了地铁某标段全长3900米的施工任务,分别从南,北两个方向同时向前掘进。已知甲工程队比乙工程队平均每天多掘进0.4米经过13天的施工两个工程队共掘进了156米.
(1)求甲,乙两个工程队平均每天各掘进多少米?
(2)为加快工程进度两工程队都改进了施工技术,在剩余的工程中,甲工程队平均每天能比原来多掘进0.4米,乙工程队平均每天能比原来多掘进0.6米,按此施工进度能够比原来少用多少天完成任务呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com