
【题目】如图,AD是△ABC的角平分线,将△ABC折叠使点A落在点D处,折痕为EF,则四边形AEDF一定是( )

A. 矩形 B. 菱形 C. 正方形 D. 梯形
【答案】B
【解析】分析:由△ABC折叠使点A落在点D处,折痕为EF,得到∠EAD=∠EDA,∠FAD=∠FDA,根据角平分线的性质推出∠FDA=∠EAD,∠FAD=∠EDA,证出平行四边形AEDF,根据折叠得到AD⊥EF,根据菱形的判定即可得出答案
解答:解:∵将△ABC折叠使点A落在点D处,折痕为EF,
∴∠EAD=∠EDA,∠FAD=∠FDA,
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∴∠FDA=∠EAD,∠FAD=∠EDA,
∴AE∥DF,DE∥AF,
∴四边形AEDF是平行四边形,
∵将△ABC折叠使点A落在点D处,折痕为EF,
∴∠AOE=∠DOE=90°,
即:AD⊥EF,
∴平行四边形AEDF是菱形.
故选B.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】已知点![]() 是直线
是直线![]() 上的一点,
上的一点,![]() ,
,![]() 平分
平分![]() .
.

(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图1中,若![]() ,直接写出
,直接写出![]() 的度数(用含
的度数(用含![]() 的式子表示);
的式子表示);
(3)将图1中的![]() 绕顶点
绕顶点![]() 逆时针旋转至图2的位置,其他条件不变,那么(2)中的求的结论是否还成立?请说明理由.
逆时针旋转至图2的位置,其他条件不变,那么(2)中的求的结论是否还成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了![]() 市
市![]() 户居民全年月平均用电量(单位:千瓦时)数据如下:
户居民全年月平均用电量(单位:千瓦时)数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表:
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
| ||
| ||
|
| |
|
| |
|
| |
合计 |
|
|
画出频数分布直方图,如下:

(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图,则不低于![]() 千瓦时的部分圆心角的度数为_____________;
千瓦时的部分圆心角的度数为_____________;
(3)若![]() 市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
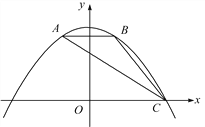
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图,A.B.C为数轴上三点,若点C到A的距离是点C到B的距离的2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为-1,点B表示的数为2.表示数1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示数0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

(1)数 所表示的点是(M,N)的好点;
(2)现有一只电子蚂蚁P从点N出发,以每秒2个单位的速度沿数轴向左运动,运动时间为t.当t为何值时,P、M、N中恰有一个点为其余两点的好点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com