
【题目】元旦期间某商店进行促销活动,活动方式有如下两种:
方式一:每满200元减50元;
方式二:若标价不超过400元时,打8折;若标价超过400元,则不超过400元的部分打8折,超出400元的部分打6折.
设某一商品的标价为![]() 元:
元:
(1)当![]() 元,按方式二应付多少钱.
元,按方式二应付多少钱.
(2)当![]() 时,
时,![]() 取何值两种方式的优惠相同.
取何值两种方式的优惠相同.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】数学问题:计算![]() (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算![]() .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() .
.

探究二:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() ,
,
两边同除以2,得![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ﹣
﹣![]() .
.

探究三:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式:_________,
所以,![]() +
+![]() +
+![]() +…+
+…+![]() =________.
=________.
拓广应用:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,某活动小组用棋子摆出了下列图形:
![]()


 ……
……
第1个图形 第2个图形 第3个图形 第4个图形
(1)探索新知:
①第![]() 个图形需要_________枚棋子;②第
个图形需要_________枚棋子;②第![]() 个图形需要__________枚棋子.
个图形需要__________枚棋子.
(2)思维拓展:
小明说:“我要用![]() 枚棋子摆出一个符合以上规律的图形”,你认为小明能摆出吗?如果能摆出,请问摆出的是第几个图形;如果不能,请说明理由.
枚棋子摆出一个符合以上规律的图形”,你认为小明能摆出吗?如果能摆出,请问摆出的是第几个图形;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
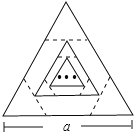
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年“双十一”购物活动,商家都会利用这个契机进行打折满减的促销活动.某商家平时的优惠措施是按所有商品标价打七折:“双十一”活动期间的优惠措施是:购买的所有商品先按标价总和打七五折,再享受折后每满![]() 元减
元减![]() 元的优惠.如标价为
元的优惠.如标价为![]() 元的商品,折后为
元的商品,折后为![]() 元,再减
元,再减![]() 元,即实付:
元,即实付:![]() (元).
(元).
(1)该商店标价总和为![]() 元的商品,在“双十一”购买,最后实际支付只需多少元?
元的商品,在“双十一”购买,最后实际支付只需多少元?
(2)小明妈妈在这次活动中打算购买某件商品,打折满减后,应付金额是![]() 元,求该商品的标价.
元,求该商品的标价.
(3)在(2)的条件下,若该商家出售的商品标价均为整数,小明通过计算后告诉妈妈:通过凑单(再购买少量商品)实际支付金额只需再多付 元,就可获得最大优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
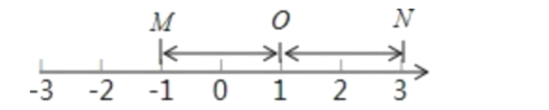
【题目】在数轴上,把表示数1的点称为基准点,记作点![]() .对于两个不同的点M和N,若点M、点N到点
.对于两个不同的点M和N,若点M、点N到点![]() 的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点
的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点![]() 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b=_________;若a=4,则b=_________;
②用含a的式子表示b,则b=____________;
(2)对点A进行如下操作:先把点A表示的数乘以2.5,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是___________;
(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,…,依此顺序不断地重复,得到
的基准变换点,…,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .
.![]() 为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
,![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,…,依此顺序不断地重复,得到
,…,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .若无论k为何值,
.若无论k为何值,![]() 与
与![]() 两点间的距离都是4,则n=__________
两点间的距离都是4,则n=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长![]() (单位长度)。慢车长
(单位长度)。慢车长![]() (单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点
(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点![]() 为原点,取向右方向为正方向画数轴,此时快车
为原点,取向右方向为正方向画数轴,此时快车![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,慢车头
,慢车头![]() 在数轴上表示的数是
在数轴上表示的数是![]() ,若快车
,若快车![]() 以
以![]() 个单位长度/秒的速度向右匀速继续行驶,同时慢车
个单位长度/秒的速度向右匀速继续行驶,同时慢车![]() 以
以![]() 个单位长度/秒的速度向左匀速继续行驶,且
个单位长度/秒的速度向左匀速继续行驶,且![]() 与
与![]() 互为相反数.
互为相反数.
(1)求此时刻快车头![]() 与慢车头
与慢车头![]() 之间相距多少单位长度?
之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒两列火车行驶到车头![]() 、
、![]() 相距
相距![]() 个单位长度?
个单位长度?
(3)此时在快车![]() 上有一位爱到脑筋的七年级学生乘客
上有一位爱到脑筋的七年级学生乘客![]() ,他发现行驶中有一段时间,他的位置
,他发现行驶中有一段时间,他的位置![]() 到两列火车头
到两列火车头![]() 、
、![]() 的距离和加上到两列火车尾
的距离和加上到两列火车尾![]() 、
、![]() 的距离和是一个不变的值(即
的距离和是一个不变的值(即![]() 为定值),你认为学生
为定值),你认为学生![]() 发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.
发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.
![]()
附加题:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com