
分析 (1)利用题中的新定义计算,即可求出x的值;
(2)不等式利用题中的新定义变形,即可求出解集;
(3)利用题中的新定义化简原式,计算即可得到结果.
解答 解:(1)由题中的新定义得:$\frac{5}{x}$-$\frac{2x}{x-3}$=-2,
去分母得:5x-15-2x2=-2x2+6x,
解得:x=-15,
经检验x=-15是分式方程的解;
(2)已知不等式变形得:-1<-2x-3(x-3)≤4,
整理得:1≤x<2;
(3)根据题中的新定义得:原式=a(a2-1)-1×(a-1)+1×(1-a)=a3-a-a+1+1-a=a3-3a+2.
点评 此题考查了解分式方程,以及解一元一次不等式组,弄清题中的新定义是解本题的关键.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
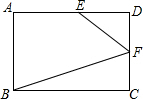 已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF,若AB=4,BC=5,则AE=$\frac{29}{10}$.
已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF,若AB=4,BC=5,则AE=$\frac{29}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
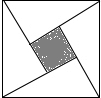 由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )
由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )| A. | 1 | B. | 3 | C. | 4-2$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com