
【题目】如图,点D为射线CB上一点,且不与点B、C重合,DE∥AB交直线AC于点E,DF∥AC交直线AB于点F.画出符合题意的图形,猜想∠EDF与∠BAC的数量关系,并说明理由.

【答案】当点D在线段CB上时,∠EDF=∠BAC;当点D在线段CB的延长线上时,∠EDF+∠BAC=180°,证明见解析.
【解析】
①当点![]() 在线段CB上时,因为DE∥AB,两直线平行,同位角相等,所以∠BAC=∠1;因为DF∥AC,两直线平行,内错角相等,所以∠EDF=∠1。等量代换,即可证明∠EDF=∠BAC;②当点D在线段CB的延长线上时,因为DF∥AC,两直线平行,内错角相等且同旁内角和为180°,所以∠BAC=∠AFD,∠EDF+∠AFD=180°。等量代换,即可证明∠EDF+∠BAC=180°。
在线段CB上时,因为DE∥AB,两直线平行,同位角相等,所以∠BAC=∠1;因为DF∥AC,两直线平行,内错角相等,所以∠EDF=∠1。等量代换,即可证明∠EDF=∠BAC;②当点D在线段CB的延长线上时,因为DF∥AC,两直线平行,内错角相等且同旁内角和为180°,所以∠BAC=∠AFD,∠EDF+∠AFD=180°。等量代换,即可证明∠EDF+∠BAC=180°。
证明:(1)如图1,2所示:
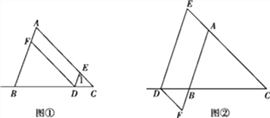
①当点D在线段CB上时,如图1,∠EDF=∠A,
证明:∵DE∥AB(已知),
∴∠1=∠BAC(两直线平行,同位角相等).
∵DF∥AC(已知),
∴∠EDF=∠1(两直线平行,内错角相等).
∴∠EDF=∠BAC(等量代换).
②当点D在线段CB的延长线上时,
如图②,∠EDF+∠BAC=180° ,
证明:∵DE∥AB(已知),
∴∠EDF+∠F=180°(两直线平行,同旁内角互补).
∵DF∥AC(已知),
∴∠F=∠BAC(两直线平行,内错角相等).
∴∠EDF+∠BAC=180°(等量代换).


科目:初中数学 来源: 题型:
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌轿车以![]() 匀速行驶的耗油情况,进行了试验:该轿车油箱加满后,以
匀速行驶的耗油情况,进行了试验:该轿车油箱加满后,以![]() 的速度匀速行驶,数据记录如下表:
的速度匀速行驶,数据记录如下表:
轿车行驶的路程 | 0 | 100 | 200 | 300 | … |
油箱剩余油量 | 50 | 41 | 32 | 23 | … |
(1)上表反映了哪两个变量之间的关系?自变量、因变量各是什么?
(2)油箱剩余油量![]() (升)与轿车行驶的路程
(升)与轿车行驶的路程![]() (千米)之间的关系式是什么?
(千米)之间的关系式是什么?
(3)若小明将油箱加满后,驾驶该轿车以![]() 的速度匀速从
的速度匀速从![]() 地驶往
地驶往![]() 地,到达
地,到达![]() 地时油箱剩余油量为5升,求两地之间的距离.
地时油箱剩余油量为5升,求两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
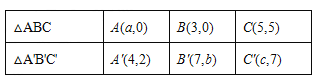
【题目】已知△A'B'C'是由△ABC经过平移得到的,它们的顶点在平面直角坐标系中的坐标如下表所示:
(1)观察表中各对应点坐标的变化,并填空:
a= , b= ,c= ;
(2)在平面直角坐标系中画出△ABC及平移后的△A'B'C';(3)△A'B'C'的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣![]() x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
(1)求m的值及点E、F的坐标;
(2)求△APE的面积;
(3)若B点是x轴上的动点,问在直线EF上,是否存在点Q(Q与A不重合),使△BEQ与△APE全等?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C表示某旅游景区三个缆车站的位置,线段AB,BC表示连接缆车站的钢缆,已知A,B,C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米,310米,710米,钢缆AB的坡度i1=1∶2,钢缆BC的坡度i2=1∶1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)

【答案】钢缆AC的长度为1 000米.
【解析】试题分析:过点A作AE⊥CC′于点E,交BB′于点F,过点B作BD⊥CC′于点D,分别求出AE、CE,利用勾股定理求解AC即可.
试题解析:过点A作AE⊥CC′于点E,交BB′于点F,过点B作BD⊥CC′于点D,
则△AFB、△BDC、△AEC都是直角三角形,四边形AA′B′F,BB′C′D和BFED都是矩形,
∴BF=BB′-B′F=BB′-AA′=310-110=200,
CD=CC′-C′D=CC′-BB′=710-310=400,
∵i1=1:2,i2=1:1,
∴AF=2BF=400,BD=CD=400,
又∵EF=BD=400,DE=BF=200,
∴AE=AF+EF=800,CE=CD+DE=600,
∴在Rt△AEC中,AC=![]() (米).
(米).
答:钢缆AC的长度是1000米.
考点:解直角三角形的应用-坡度坡角问题.
【题型】解答题
【结束】
24
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )

A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com