
分析 (1)把点P的坐标代入直线方程求得a的值;然后将点P的坐标代入抛物线方程来求c的值;
(2)设抛物线y=$\frac{1}{4}$x2+3沿着y轴方向平移b个单位长度后得y-b=y=x2+3则得方程-2x-b=y=$\frac{1}{4}$x2++3,得到△=82-4(4b+12)=16-16k,然后令16-16b=0,解得:b=1,从而确定平移的方向和单位.
解答 解:(1)∵点P(a,4)在直线y=-2x上,
∴4=-2a,
即:a=-2,
又∵点P(-2,4)在抛物线y=$\frac{1}{4}$x2+c上,
∴4=$\frac{1}{4}$×(-2)2+c,
即:c=3;
(2)把已知的二次函数的图象沿着y轴方向向上平移1个单位长度,所得的图象与直线y=-2x有且只有一个公共点.
理由:由(1)知,抛物线y=$\frac{1}{4}$x2+3和直线y=-2x有两个公共点,
因此设抛物线y=$\frac{1}{4}$x2+3向上平移b个单位长度后得y-b=y=$\frac{1}{4}$x2+3,
则得方程-2x-b=y=$\frac{1}{4}$x2+3,
即:x2+8x+4b+12=0,
△=82-4(4b+12)=16-16k,
令16-16b=0,解得:k=1,
故把已知的二次函数的图象沿着y轴方向向上平移1个单位长度,所得的图象与直线y=-2x有且只有一个公共点.
点评 本题考查了二次函数的性质及二次函数的图象与几何变换的知识,解题的关键是确定二次函数的解析式,难度中等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在同圆或等圆中,若两弧相等,则他们所对的弦相等 | |
| B. | 在同一个圆中,若弦长等于半径,则该弦所对的劣弧的度数为60° | |
| C. | 在同一个圆中,若两弧不等,则大弧所对的圆心角较大 | |
| D. | 若两弧的度数相等,则这两条弧是等弧 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在△ABC中,直线MN是AC的垂直平分线,若CM=4cm,△ABC的周长是27cm,那么△ABN的周长是( )
如图所示,在△ABC中,直线MN是AC的垂直平分线,若CM=4cm,△ABC的周长是27cm,那么△ABN的周长是( )| A. | 19cm | B. | 17cm | C. | 9cm | D. | 9cm或17cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
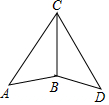 如图,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( )
如图,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是( )| A. | △ABC≌△DBC | B. | ∠A=∠D | ||
| C. | BC是∠ACD的平分线 | D. | ∠A=∠BCD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com