
阅读下列一段话,并解决后面的问题.
观察下面一列数:
1,2,4,8,16,32…
我们发现,这一列数从第2项起,每一项与它前一项的比都是2,即
一般地,如果一列数从第2项起,每一项与它前一项的比都等于同一个常数,这个数列就叫做等比数列,这一常数就叫做等比数列的公比,例如上面数列的比值2即为这个数列的公比.问:
①等比数列﹣1,3,﹣9,27,…的公比是__________,第五项是__________.
②如果一列数a1,a2,a3,a4,…是等比数列,且公比为q,那么根据上述的规定,有 ,
, =q,
=q, ,…所以a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,…an=__________.(用a1,q,n的代数式表示)
,…所以a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,…an=__________.(用a1,q,n的代数式表示)
③一个等比数列的第二项是8,公比是﹣ ,则第八项是__________.
,则第八项是__________.
【考点】规律型:数字的变化类.
【专题】规律型.
【分析】(1)根据题意可得等比数列5,﹣15,45,…中,从第2项起,每一项与它前一项的比都等于﹣3;故第4项是45×(﹣3)=﹣135;
(2)观察数据可得an=a1qn﹣1;
(3)根据(1)中的定义,与(2)的关系式, 可得它的第八项的值.
可得它的第八项的值.
【解答】解:①3÷(﹣1)=﹣3,27×(﹣3)=﹣81;
②an=a1qn﹣1;
③8×(﹣ )6=
)6=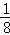 .
.
故答案为:﹣3,﹣81;a1qn﹣1;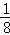 .
.
【点评】本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.分析数据获取信息是必须掌握的数学能力,如观察数据可得an=a1qn﹣1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
下列说法中正确的是( )
A.正数和负数统称有理数
B.相反数大于本身的数是负数
C.(﹣1)n+(﹣1)n﹣1=﹣1(n是大于1的整数)
D.若|a|=|b|,则a=b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com