
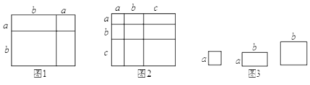
【题目】(知识生成)我们已经知道,对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2请解答下列问题:
(1)写出图2中所表示的数学等式________________;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a,b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z=_______;
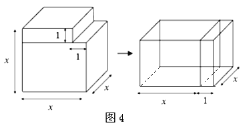
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个数学等式:_______________.
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)45;(3)x+y+z=9;(4)![]() .
.
【解析】
(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.
(2)根据利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出.
(3)找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件.
(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)由(1)得:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
∵a+b+c=11,ab+bc+ac=38
∴121=a2+b2+c2+2×38,所以a2+b2+c2=121-76=45.
(3)(a+2b)(2a+b)=2a2+2b2+5ab,
所以x=2,y=2,z=5,所以x+y+z=9.
(4)x3-x=x(x-1)(x+1).


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有【 】个.

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥NN于点M,BN⊥MN于N.
(1)求证:△AMC≌△CNB;
(2)求证:MN=AM+BN.

查看答案和解析>>
科目:初中数学 来源: 题型:
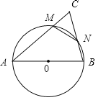
【题目】如图,以![]() 的边
的边![]() 为直径画圆,与边
为直径画圆,与边![]() 交于
交于![]() ,与边
,与边![]() 交于
交于![]() ,已知
,已知![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,
倍,![]() 中有一个内角度数是另一内角度数的
中有一个内角度数是另一内角度数的![]() 倍,试计算
倍,试计算![]() 三个内角的度数:________.
三个内角的度数:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,以
,以![]() 为直径,
为直径,![]() 为圆心的半圆交
为圆心的半圆交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的角平分线,且
的角平分线,且![]() ,垂足为点
,垂足为点![]() .
.
![]() 判断直线
判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有![]() 、
、![]() 两种商品,
两种商品,![]() 商品每件售价
商品每件售价![]() 元,
元,![]() 商品每件售价
商品每件售价![]() 元,
元,![]() 商品每件的成本是
商品每件的成本是![]() 元.
元.
根据市场调查“若按上述售价销售,该商场每天可以销售![]() 商品
商品![]() 件,若销售单价毎上涨
件,若销售单价毎上涨![]() 元,
元,![]() 商品每天的销售量就减少
商品每天的销售量就减少![]() 件.
件.
![]() 请写出
请写出![]() 商品每天的销售利润
商品每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() 元之间的函数关系?
元之间的函数关系?
![]() 当销售单价为多少元时,
当销售单价为多少元时,![]() 商品每天的销售利润最大,最大利润是多少?
商品每天的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
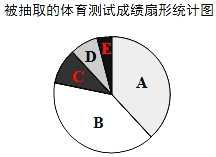
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市南湖生态城某楼盘准备以每平方米![]() 元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米
元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米![]() 元的均价开盘销售.
元的均价开盘销售.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 王先生准备以开盘价均价购买一套
王先生准备以开盘价均价购买一套![]() 平方米的住房,开发商给予以下两种优惠方案:
平方米的住房,开发商给予以下两种优惠方案:
①打![]() 折销售;
折销售;
②不打折,一次性送装修费每平方米![]() 元,试问那种方案更优惠?
元,试问那种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知关于x的一元二次方程x2+2x+![]() =0有两个不相等的实数根,k为正整数.
=0有两个不相等的实数根,k为正整数.
(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+![]() 的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com