
【题目】如图,已知关于x的一元二次方程x2+2x+![]() =0有两个不相等的实数根,k为正整数.
=0有两个不相等的实数根,k为正整数.
(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+![]() 的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.

【答案】(1)k=1或2;(2)当t=﹣![]() 时,MN有最大值,最大值为
时,MN有最大值,最大值为![]() .
.
【解析】
(1)、根据方程有两个不相等的实数根得出△>0,从而得出k的取值范围,然后根据k为正整数,从而得出k的值;(2)、将x=0代入方程求出k的值,从而得出函数解析式,解出函数的交点坐标,设M(t,t+2)(﹣2<t<1),则N(t,t2+2t),然后根据长度的计算法则得出函数解析式,从而得出最大值.
(1)根据题意得△=22﹣4×![]() >0,解得k<3,而k为正整数, 所以k=1或2;
>0,解得k<3,而k为正整数, 所以k=1或2;
(2)当x=0代入x2+2x+![]() =0得k=1,则方程为x2+2x=0, 二次函数为y=x2+2x,
=0得k=1,则方程为x2+2x=0, 二次函数为y=x2+2x,
解方程组![]() 得
得![]() 或
或![]() ,则A(﹣2,0),B(1,3),
,则A(﹣2,0),B(1,3),
设M(t,t+2)(﹣2<t<1),则N(t,t2+2t),
所以MN=t+2﹣(t2+2t)=﹣t2﹣t+2=﹣(t+![]() )2+
)2+![]() ,
,
当t=﹣![]() 时,MN有最大值,最大值为
时,MN有最大值,最大值为![]() .
.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】(知识生成)我们已经知道,对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2请解答下列问题:
(1)写出图2中所表示的数学等式________________;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a,b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z=_______;
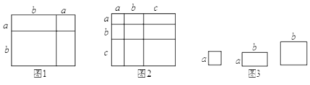
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个数学等式:_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,AB=7,AD=2,BC=3,如果边AB上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,则这样的P点共有几个( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 中位数就是一组数据中最中间的一个数
B. ![]() 这组数据的众数是9
这组数据的众数是9
C. 如果![]() 的平均数是1,那么
的平均数是1,那么![]()
D. 一组数据的方差是这组数据的极差的平方
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为0.7米.如果梯子的顶端沿墙面下滑0.4米,那么点B将向左滑动多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:观察下列各式:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)猜想![]() 的变形结果并验证;
的变形结果并验证;
(2)针对上述各式反映的规律,给出用![]() (
(![]() 为任意自然数,且
为任意自然数,且![]() )表示的等式,并进行证明.
)表示的等式,并进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )的对称轴为直线
)的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,其部分图象如图所示,下列结论:①
,其部分图象如图所示,下列结论:①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;⑤当
;⑤当![]() 时,
时,![]() 随
随![]() 增大而增大.其中结论正确的个数是( )
增大而增大.其中结论正确的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com