
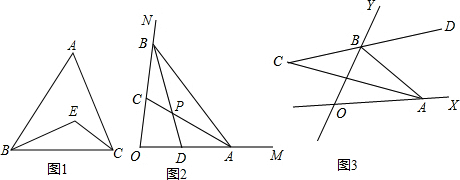
分析 (1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的定义得出∠EBC+∠ECB的度数,由三角形内角和定理即可得出结论;
(2)先根据三角形内角和定理及角平分线的性质求出∠APB的度数,再根据三角形内角和是180°即可求解;
(3)令∠OAC=∠CAB=x,∠ABD=∠BDY=y,再根据三角形的外角性质即可求解.
解答 解:(1)∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°.
∵点E是两条内角平分线的交点,
∴∠EBC+∠ECB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×120°=60°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-60°=120°;
(2)不变.
∵在△AOB中,∠MON=80°,
∴∠OAB+∠OBA=100°,
又∵AC、BD为角平分线,
∴∠PAB+∠PBA=$\frac{1}{2}$∠OAB+$\frac{1}{2}$∠OBA=$\frac{1}{2}$×100°=50°,
∴∠APB=180°-(∠PAB+∠PBA)=130°,
即随着点A、B位置的变化,∠APB的大小始终不变,为130°;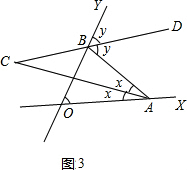
(3)不变.
令∠OAC=∠CAB=x,∠ABD=∠BDY=y,
∵∠ABY是△AOB的外角,
∴2y=n+2x,
同理,∠ABD是△ABC的外角,有y=∠C+x,
∴∠C=$\frac{∠XOY}{2}$=$\frac{60°}{2}$=30°.
点评 本题考查的是三角形的内角和定理及三角形外角的性质,解答此题的关键是熟知以下知识:①三角形的外角等于与之不相邻的两个内角的和;②三角形的内角和是180°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
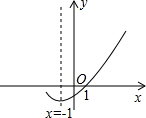 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com