Question

如图，用同样规格黑白两色的正方形瓷砖铺设长方形地面，请观察下列图形，并解答有关问题：

（1）铺设地面所用瓷砖的总块数为______（用含n的代数式表示，n表示第n个图形）；
（2）按上述铺设方案，铺一块这样的长方形地面共用了506块瓷砖，求此时n的值；
（3）是否存在黑瓷砖与白瓷砖块数相等的情形？请通过计算加以说明．

Answer 1

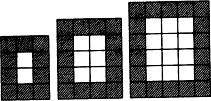
解：（1）第一个图形用的正方形的个数=3×4=12，第二个图形用的正方形的个数=4×5=20，第三个图形用的正方形的个数=5×6=30…以此类推，第n个图形用的正方形的个数=（n+2）（n+3）个；
故答案为：n²+5n+6或（n+2）（n+3）；

（2）根据题意得：n²+5n+6=506，
解得n₁=20，n₂=-25（不符合题意，舍去）；

（3）根据题意得：n（n+1）=2（2n+3），
解得n=（不符合题意，舍去），
∴不存在黑瓷砖与白瓷砖块数相等的情形．
分析：（1）第一个图形用的正方形的个数=3×4=12，第二个图形用的正方形的个数=4×5=20，第三个图形用的正方形的个数=5×6=30…以此类推，第n个图形用的正方形的个数=（n+2）（n+3）个；
（2）根据题意可得（n+2）（n+3）=506，解关于n的一元二次方程即可；
（3）第一个图形中白色瓷块有1×2=2，黑色瓷块=2×5=10，
第二个图形中白色瓷块有2×3=6，黑色瓷块=2×7=14，
第三个图形中白色瓷块有3×4=12，黑色瓷块=2×9=18…
那么依此类推第n个图形中有白色瓷块=n（n+1），黑色瓷块=2（2n+3），根据题意可得n（n+1）=2（2n+3），解关于n的方程即可．
点评：本题考查了一元二次方程的应用，解题的关键主要是寻找规律，还使用了解一元二次方程的知识．