
【题目】(1)![]() ;
;
(2)![]() ;
;
(3)先化简,再求值![]() ,其中
,其中![]() 与
与![]() 互为相反数.
互为相反数.
【答案】(1)![]() (2)8(3)-6
(2)8(3)-6
【解析】
(1)原式先计算乘方运算和绝对值,再计算乘除运算,最后算加减运算即可得到结果;
(2)原式利用除法法则变形,再利用乘法分配律计算即可得到结果;
(3)原式去括号合并得到最简结果,根据已知条件求出a、b的值,再把a与b的值代入最简结果,计算即可求出值.
解:(1)![]()
=-8-0.5×![]() ×(2-9)
×(2-9)
=-8-0.5×![]() ×(-7)
×(-7)
=-8+![]()
=-![]() ;
;
(2)![]()
=![]()
=(![]() )
)![]() (
(![]() )
)![]()
=12+16-20
=8;
(3)![]() ,
,
=-3ab+3a2-[2b2-5ab+a2-2ab]
=-3ab+3a2-2b2+5ab-a2+2ab
=2a2-2b2+4ab
∵![]() 与
与![]() 互为相反数.
互为相反数.
∴![]() +
+![]() =0
=0
∴![]() =0,
=0,![]() =0
=0
∴![]() =1,
=1,![]() =-2
=-2
∴原式=4![]() +2(
+2(![]() )=-6
)=-6


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
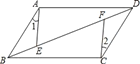
A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若∠BAC=90°,AC平分∠EAF,且BC=8cm,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
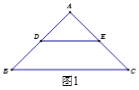
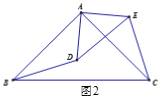
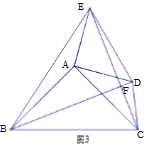
【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D、E在AB、AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点. 若BD=![]() ,求四边形BCDE的面积.
,求四边形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,某学习小组对有一内角(∠BAD)为120°的平行四边形ABCD,将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究:在(2)的条件下,学习小组某成员探究发现AE+2AF= ![]() AC,试判断结论是否正确,并说明理由.
AC,试判断结论是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交 ![]() 于点E,以点O为圆心,OC的长为半径作
于点E,以点O为圆心,OC的长为半径作 ![]() 交OB于点D.若OA=2,则阴影部分的面积为 .
交OB于点D.若OA=2,则阴影部分的面积为 . 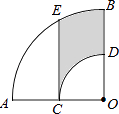
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的半圆上,AB=4 ![]() ,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是 .
,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是 . 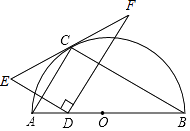
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com