
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交 ![]() 于点E,以点O为圆心,OC的长为半径作
于点E,以点O为圆心,OC的长为半径作 ![]() 交OB于点D.若OA=2,则阴影部分的面积为 .
交OB于点D.若OA=2,则阴影部分的面积为 . 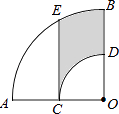
科目:初中数学 来源: 题型:
【题目】已知:c=10,且a,b满足(a+26)2+|b+c|=0,请回答问题:
(1)请直接写出a,b,c的值:a= ,b= ;
(2)在数轴上a、b、c所对应的点分别为A、B、C,记A、B两点间的距离为AB,则AB= ,AC= ;
(3)在(1)(2)的条件下,若点M从点A出发,以每秒1个单位长度的速度向右运动,当点M到达点C时,点M停止;当点M运动到点B时,点N从点A出发,以每秒3个单位长度向右运动,点N到达点C后,再立即以同样的速度返回,当点N到达点A时,点N停止.从点M开始运动时起,至点M、N均停止运动为止,设时间为t秒,请用含t的代数式表示M,N两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的数阵是由88个偶数组成:
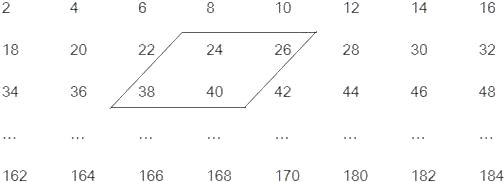
(1)观察数阵中平行四边形框内的四个数之间的关系,在数阵中任意作一个相同的平行四边形框圈出四个数,设其中最小的数为x,那么其他三个数怎样表示?
(2)甲同学这样圈出的四个数的和为432,你能求出这四个数吗?
(3)乙同学想用这样的框圈出和为172的四个数,可能吗?
(4)你能用这样的框圈出和为352的四个数吗?若能,请写出这四个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红学习了用图形面积研究整式乘法的方法后,分别进行了如下数学探究:把一根铁丝截成两段,
探究1:小明截成了两根长度不同的铁丝,并用两根不同长度的铁丝分别围成两个正方形,已知两正方形的边长和为20cm,它们的面积的差为40cm2,则这两个正方形的边长差为 .
探究2:小红截成了两根长度相同的铁丝,并用两根同样长的铁丝分别围成一个长方形与一个正方形,若长方形的长为xm,宽为ym,
(1)用含x、y的代数式表示正方形的边长为 ;
(2)设长方形的长大于宽,比较正方形与长方形面积哪个大,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
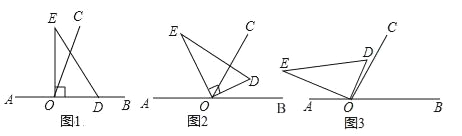
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠DAB下列条件中不能使△ABC≌△ABD的是( )

A. ∠C=∠D B. ∠ABC=∠ABD C. AC=AD D. BC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1) 如图1,当∠BOC=70°时,求∠DOE的度数.
(2) 如图2,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?说明理由.
(3) 当射线OC在∠AOB外绕点O旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数.(不必写出过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com