
【题目】已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】某市“每天锻炼一小时,幸福生活一辈子”活动已开展了一年,为了解该市此项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取200名居民;
B.从一个城镇的不同住宅楼中随机选取200名居民;
C.从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象,然后进行调查.
(1)在上述调查方式中,你认为比较合理的一个是 (填序号).
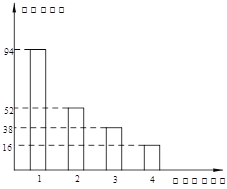
(2)由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图,在这个调查中,这200名居民每天锻炼2小时的人数是多少?
(3)若该市有l00万人,请你利用(2)中的调查结果,估计该市每天锻炼2小时及以上的人数是多少?
(4)你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
小明遇到这样一个问题:求计算![]() 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算![]() 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找![]() 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:

也就是说,只需用![]() 中的一次项系数1乘以
中的一次项系数1乘以![]() 中的常数项3,再用
中的常数项3,再用![]() 中的常数项2乘以
中的常数项2乘以![]() 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加![]() ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算![]() 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用![]() 的一次项系数1,
的一次项系数1, ![]() 的常数项3,
的常数项3, ![]() 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用![]() 的一次项系数2,
的一次项系数2, ![]() 的常数项2,
的常数项2, ![]() 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用![]() 的一次项系数3,
的一次项系数3, ![]() 的常数项2,
的常数项2, ![]() 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算![]() 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则![]() =_________.
=_________.
(4)若![]() 是
是![]() 的一个因式,则
的一个因式,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一张如图①所示的长方形铁皮四个角都剪去边长为30cm的正方形,再四周折起,做成一个有底无盖的铁盒,如图②.铁盒底面长方形的长是4acm,宽是3acm.

(1)请用含有a的代数式表示图①中原长方形铁皮的面积;
(2)若要在铁盒的外表面涂上某种油漆,每1元钱可涂油漆的面积为![]() cm2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?
cm2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a的代数式表示)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( ) 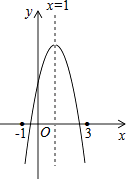
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个木箱中装有卡片共50张,这些卡片共有三种,它们分别标有1、2、3的字样,除此之外其他都相同,其中标有数字2的卡片的张数是标有数字3卡片的张数的3倍少8张.已知从箱子中随机摸出一张标有数字1卡片的概率是 ![]() .
.
(1)求木箱中装有标1的卡片张数;
(2)求从箱子中随机摸出一张标有数字3的卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了合理利用电力资源,缓解用电紧张状况,我国电力部门出台了使用“峰谷电”的政策及收费标准(见下表).
用电时间段 | 收费标准 | |
峰电 | 08:00—22:00 | 0.56元/千瓦时 |
谷电 | 22:00—08:00 | 0.28元/千瓦时 |
已知王老师家4月份使用“峰谷电”95千瓦时,缴电费43.40元,问王老师家4月份“峰电”和“谷电”各用了多少千瓦时?设王老师家4月份“峰电”用了x千瓦时,“谷电”用了y千瓦时,根据题意,列方程组得_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:c=10,且a,b满足(a+26)2+|b+c|=0,请回答问题:
(1)请直接写出a,b,c的值:a= ,b= ;
(2)在数轴上a、b、c所对应的点分别为A、B、C,记A、B两点间的距离为AB,则AB= ,AC= ;
(3)在(1)(2)的条件下,若点M从点A出发,以每秒1个单位长度的速度向右运动,当点M到达点C时,点M停止;当点M运动到点B时,点N从点A出发,以每秒3个单位长度向右运动,点N到达点C后,再立即以同样的速度返回,当点N到达点A时,点N停止.从点M开始运动时起,至点M、N均停止运动为止,设时间为t秒,请用含t的代数式表示M,N两点间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com